Binomial Theorem

Binomial theorem (or Binomial Expansion) gives us a way for finding any power of a binomial without multiplying at length.

History

1. Special cases of the binomial theorem were known since at least the 4th century BC when Greek mathematician Euclid mentioned the special case of the binomial theorem for exponent.

2. There is evidence that the binomial theorem for cubes was known by the 6th century AD in India.

3. In 1544, Michael Stifel introduced the term “binomial coefficient” and showed how to use them to express (1 + a)ⁿ in terms of (1+a)^n-1, via “Pascal’s triangle“.

Theorem

Statement (Binomial theorem formula)

According to the theorem, it is possible to expand any nonnegative power of (x + y) into a sum of the form

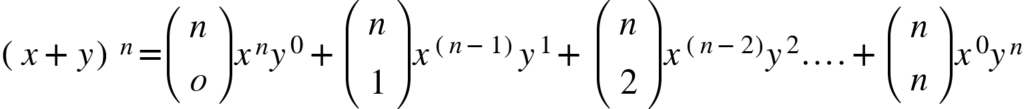
Where, \(n\geq 0\ and\ 0\leq k\leq n,\ {N\choose k}\) is a positive integer known as binomial coefficient.

Binomial Theorem Proof (by Induction)

The proof will be given by using the Principle of mathematical induction (PMI). This is done by first proving it for n=1, then assuming that it is true for n=k, we prove it for n=k.

Let P(n):

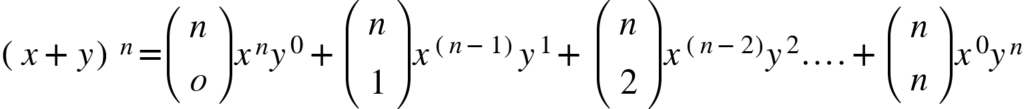
Now, for n=1 we have

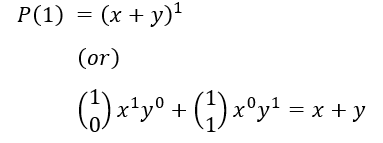
So, it’s true for n=1

Now, for n=2 we have

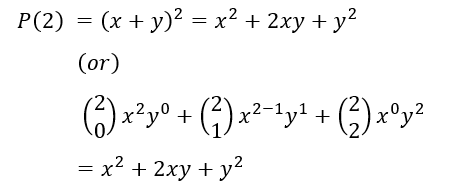
So, it’s true for n=2

Now let n=k be true, i.e.

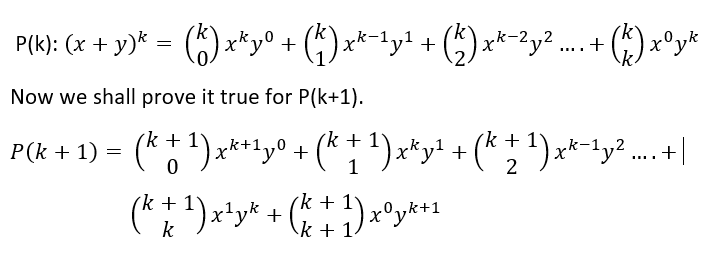
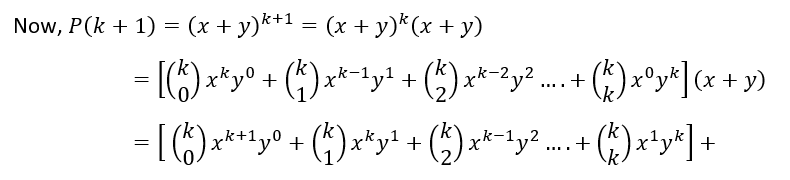
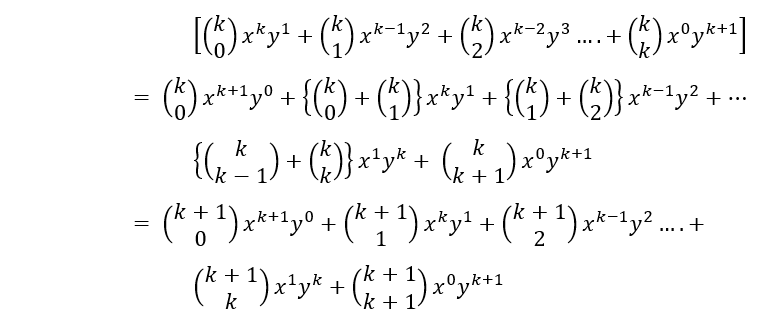
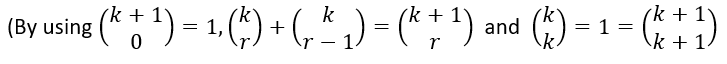
Thus, it has been proved that P(k+1) is true for all values of k.

Therefore, by principle of mathematical induction, P(n) is true for every positive integer n.

Applications

Binomial Theorem plays an important role in many different fields of mathematics as well other areas. Some of these are

1. Multiple-angle identities– In complex numbers, the binomial theorem is combined with de Moivre’s formula to yield multiple-angle formulas for the Sine and Cosine. The expression can be expanded, and then the real and imaginary parts can be taken to yield formulas.

2. Series for e– The number is defined by the formula

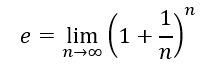
3. Probability– This theorem is closely related to the probability mass function. Binomial probability refers to the probability of exactly x successes on n repeated trials in an experiment which has two possible outcomes

Binomial Theorem Examples

1. Find an approximation of (0.99)⁵.

Sol. We can solve this by just multiplying 0.99 five times but a smart way would be by using binomial theorem in a clever way.

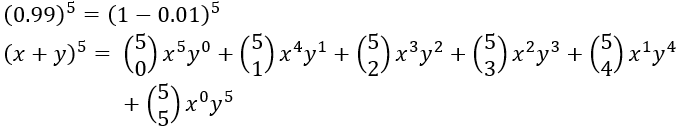
On solving the above expression we get the answer as 0.9509900499.

2. How many terms are present in the expansion of (x + a)¹⁰⁰ + (x – a)¹⁰⁰ after simplification.

Sol.

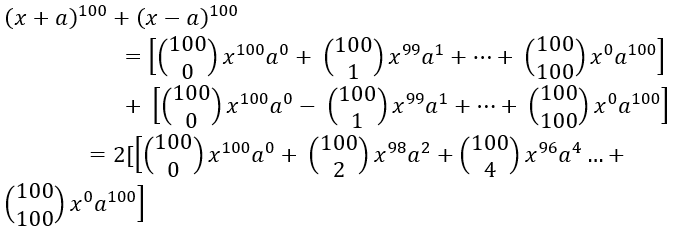
So, there are 101 terms in these expansions, and 50 odd powered (negative terms in the second expansion) gets cancelled leaving us with 51 terms.

So, the expansion will have 51 terms,

FAQs