Kepler’s Laws Of Planetary Motion

Kepler’s laws of planetary motion, are the laws that describe the motions of the planets in the solar system. These laws were derived by Johannes Kepler, a German astronomer, in the early 1600s. And hence these laws are named after him.

These laws are mainly used in Astronomy and Classical Physics.

History

Kepler was able to summarize the carefully collected data of his mentor –Tycho Brahe– a Danish astronomer. Kepler published his first two laws in 1609, in the book Astronomia Nova. The third law was published nearly a decade later, in 1619, in the book Harmonices  Mundi.

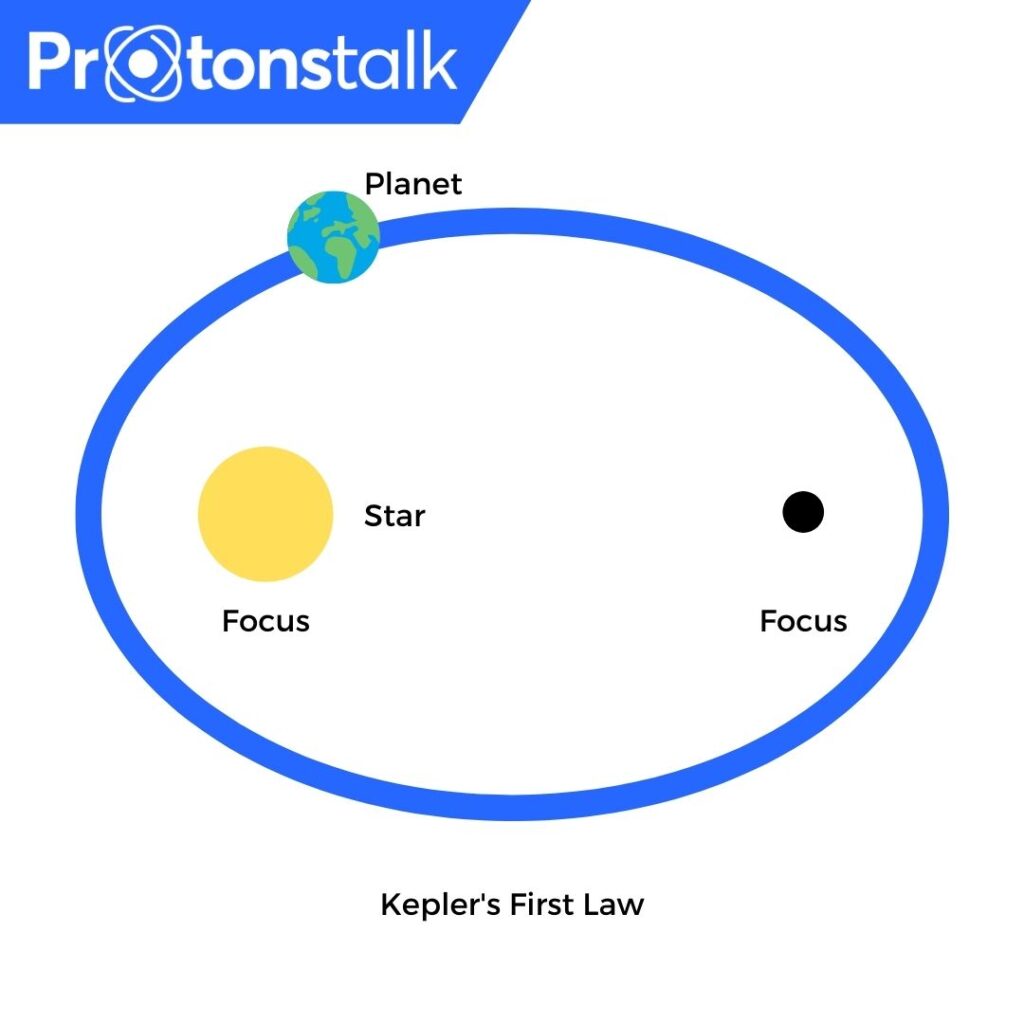
Kepler’s First Law

The path of the planets about the sun is elliptical, with the sun at one of the two foci. This is known as the law of Ellipses.

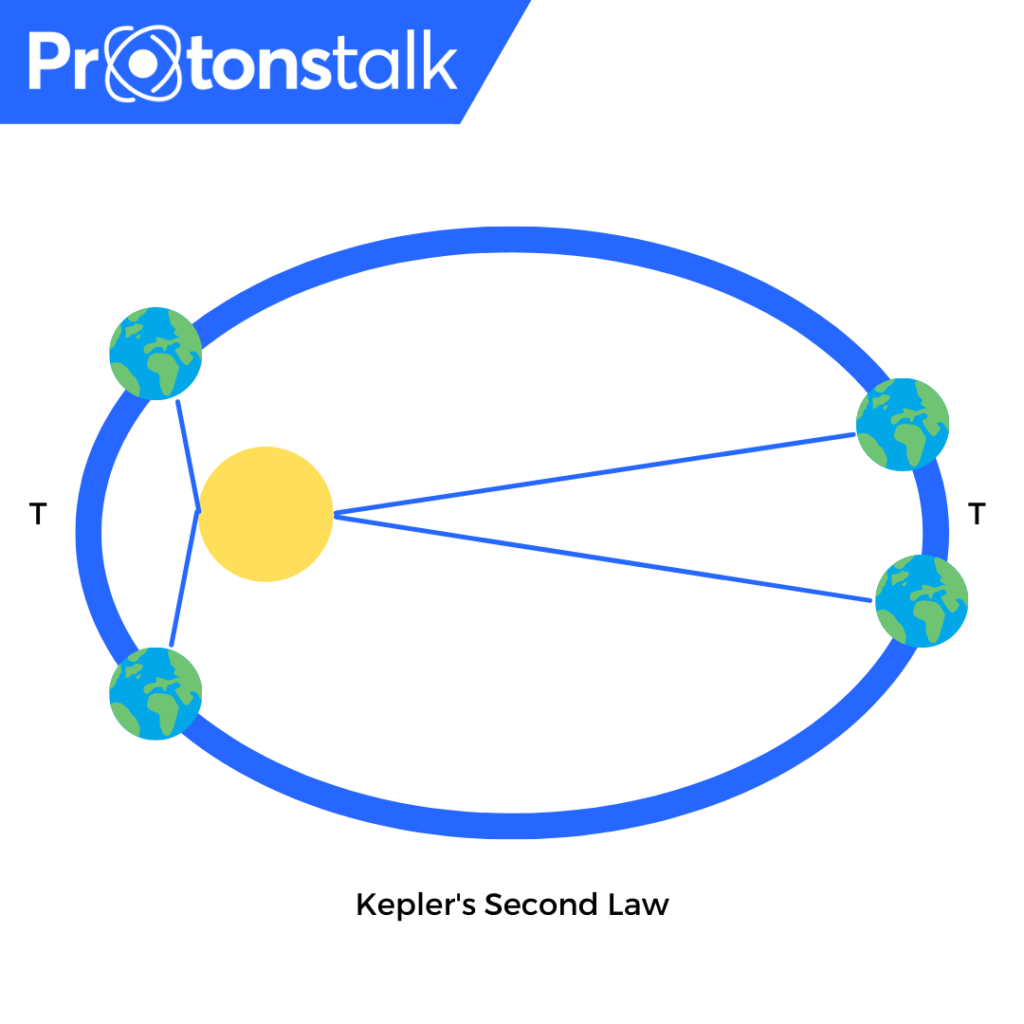
Kepler’s Second Law

An imaginary line drawn from the center of the sun to the center of the planet will sweep out equal areas in equal intervals of time. This is known as the Law of Equal areas.

Kepler’s third law

The square of a planet’s orbital period is proportional to the cube of the length of the semi-major axis of its orbit( i.e T² α R³ ).  This is known as the Law of Harmonies.

Which means..

(T₁/T₂)² = (R₁/R₂)³

Applications

• They have been used to find the orbits of many objects such as Comets and Asteroids.
• These laws played a key role in the discovery of dark matter in the Milky Way.
• Although Kepler originally developed his laws in the context of planetary orbits, the results hold valid for any system with radial force obeying the inverse square laws
• The 1^rst and the 2^nd laws help us determine the path of the objects in space.
• Whereas the third law is used to determine the period and radius of the elliptical paths.

Example Problems

Question 1: A satellite on a circular orbit of radius R around Mars has an orbital period of 10.0 hr. A second satellite is to be placed in a circular orbit so that its orbital period will be 5.00 hr. The radius of the orbit of the second satellite should be closest to?

Ans: For Satellite-1 with circular orbit about a planet:

The radius of the orbit: R

Time, T₁ = 10.0 hr

For Satellite-2 with circular orbit about the same planet:

The radius of the orbit: R’ (To be found)

Time, T₂ = 5.00 hr

 T₂² ∕ T₁² =  R’ ³ / R³

(5.00 hr)² ∕ ( 10.0 hr)² =  R’ ³ / R³ 

We get  R’ = 0.630 × R

Question 2: A satellite A of mass M is at a distance of r from the center of the earth. Another satellite B of mass 2m is at a distance of 2r from the earth’s center. Their time periods are in the ratio of ..?

Ans: Here we should note that Mass of the satellite does not affect the  time period.

We know that 

(T₁/T₂)² = (R₁/R₂)³

R₁=r;

R₂=2r;

So  we get the ratio of the time period = 1/2√ 2  sec

FAQs

So, that is all about Kepler’s laws of planetary motion.