Pascal’s Triangle is one of the interesting number patterns in mathematics. This is a triangular array constructed by summing adjacent elements in preceding rows.
Index
History
Pascal’s triangle is named after the 17th century French mathematician, Blaise Pascal (1623 – 1662), although other mathematicians studied it centuries before him in India, Persia, China, Germany, and Italy. Pascal innovated many previously unattested uses of the triangle’s numbers, uses he described comprehensively in the earliest known mathematical treatise to be specially devoted to the triangle, his Traité du triangle arithmétique (1654; published 1665).
Construction of Pascal’s Triangle
To build the triangle, start with “1” at the top, On the next row write two 1’s, forming a triangle. On each subsequent row start and end with 1’s and compute each interior term by summing the two numbers above it.
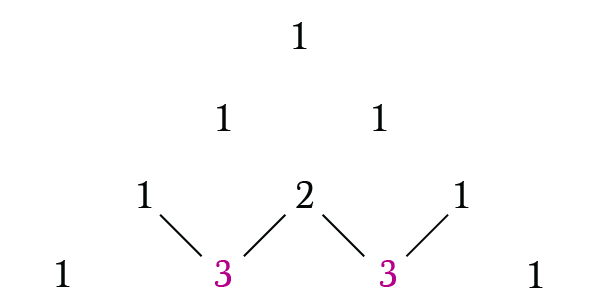
By repeating this process we will end up getting a Pascal triangle. This is a never ending triangle.
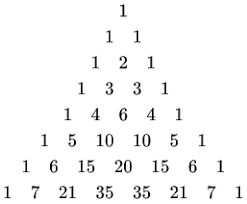
Properties of Pascal’s Triangle
- Each number is the sum of the two numbers above it.
- The triangle is symmetric.
- The diagonals going along the left and right edges contain only 1’s. The diagonals next to the edge diagonals contain the natural numbers in order. The next diagonal is the triangular numbers. Similarly, the next diagonals are the tetrahedral numbers or triangular pyramidal numbers.

- Sum the diagonals of the left-justified Pascal Triangle forms a Fibonacci Sequence
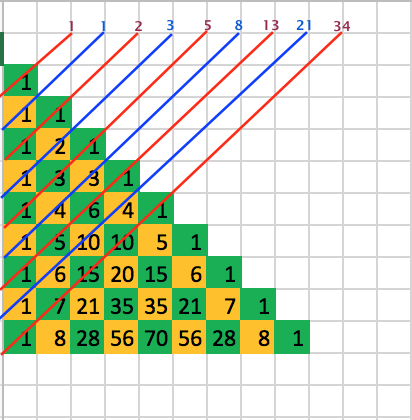
- The sums of the rows give the powers of 2.

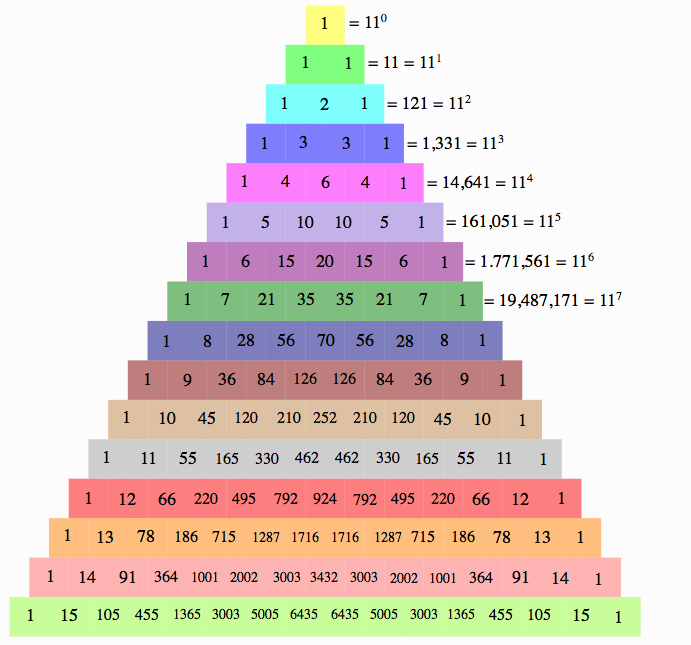
- Each row gives the digits of the powers of 11.
- Start with any number in the triangle and proceed down the diagonal. Then change the direction in the diagonal for the last number. That last number is the sum of every other number in the diagonal, this is known as Hockey Stick Pattern.

- Catalan numbers are found by taking polygons, and finding how many ways they can be partitioned into triangles. These numbers are found in Pascal’s triangle by starting in the 3 row down the middle and subtracting the number adjacent to it. (Catalan numbers are 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020)

- If you shade all the even numbers, you will get a fractal. This is also the recursive of Sierpinski’s Triangle.

Application of Pascal’s Triangle
Now let’s have a look at the application of Pascal’s triangle.
Binomial Expansion
Pascals triangle determines the coefficients which arise in binomial expansion.
Suppose you have the binomial (x + y) and you want to raise it to a power such as 2 or 3.
For Example:
Let’s expand (x+y)³. Since we’re raising (x+y) to the 3rd power, use the values in the fourth row of Pascal’s as the coefficients of your expansion. Then fill in the x and y terms as outlined below.
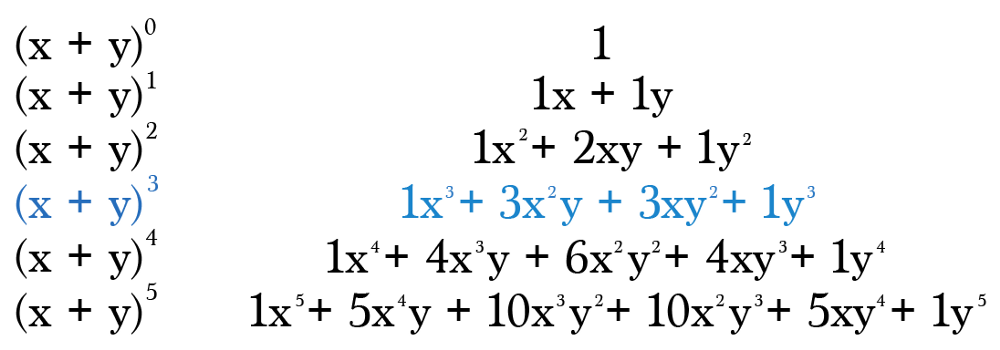
Probability
Pascals triangle can show us the way how heads and tails can combine. This gives the probability of any combination.
For Example:
If H represent heads and T represent tails then if a coin is tossed for 4 times, the possibilities of combinations are
- HHHH
- HHHT, HHTH, HTHH, THHH
- TTHH, HHTT, HTHT, HTTH,THHT, THTH
- HTTT, THTT, TTHT, TTTH
- TTTT
Thus, the observed pattern is 1,4,6,4,1. (A row in Pascal’s triangle)
Combinations
A useful application of Pascals triangle is in the calculation of combinations.
We know that If the number of combinations of n things taken k at a time (called n choose k) can be found by the equation \(C(n, k) = C^{n}_{k} = {n \choose k} = \frac{n!}{k!(n – k)!}\)
But this is a formula for an entry of a cell in Pascal’s triangle as well. So, we can just lookup that particular entry and in the triangle and find it out.
Note: For doing this, the numbering of first row and the first entry in the row should start from 0.
For example: (For finding the combination value)
Suppose a basketball team has 11 players and wants to know how many ways there are of selecting 8.
The answer is entry 8 in row 11, which is 165; that is, 11 choose 8 is 165.
(This is only when the numbering starts from 0 or else if it starts from 1 then we will have to see the 9th entry in 12the column )
Pascal’s Triangle Examples
Question 1. Expand \((a – 3b)^{4}\).
Solution:
Using the triangle the coefficients for this expansion are 1, 4, 6, 4, and 1. The signs for each term are going to alternate, because of the negative sign.
\((a – 3b)^{4}\\
= 1a^4 – 4a^3(3b) + 6a^2(3b)^2 – 4a(3b)^3 + 1(3b)^4\\
= a^4 – 12a^3b + 6a^2(9b^2) – 4a(27b^3) + 81b^4\\
=> > a^4 – 12a^3b + 54a^2b^2 – 108ab^3 + 81b^4
\)
Question 2. In Pascals Triangle, each entry is the sum of the two entries above it. In which row of the triangle do three consecutive entries occur that are in the ratio 3:4:5?
Solution: Call the row x, and the number from the leftmost side t.
Call the first term in the ratio \(N\), which is \(N = {x \choose t}\).
The next term is \(N * \frac{x – t}{t + 1}\),
and the final term is \(N * \frac{(x – t) * (x – t – 1)}{(t + 1) * (t + 2)}\).
Because we have the ratio,
\(N : N * \frac{x – t}{t + 1} : N * \frac{(x – t) * (x – t – 1)}{(t + 1) * (t + 2)} = 3 : 4 : 5\).
So, \(\frac{x – t}{t + 1} = \frac{4}{3}\) and \(\frac{(x – t) * (x – t – 1)}{(t + 1) * (t + 2)} = \frac{5}{3}\).
Solve the equation to get get t = 26 and x = 69
FAQs
Pascal’s triangle is a never-ending equilateral triangle of numbers that follow a rule of adding the two numbers above to get the number below. Two of the sides are “all 1’s” and because the triangle is infinite, there is no “bottom side.”
Pascal’s Triangle has many applications in mathematics and statistics, including its ability to help you calculate combinations.
Pascal’s triangle is named for Blaise Pascal, a French mathematician who used the triangle as part of his studies in probability theory in the 17th century. Blaise Pascal didn’t really “discover” the triangle named after him, though, it has actually been studied all over the world for thousands of years.
