The parallel and perpendicular axis theorems are used to find the moment of inertia of a rigid body about different axes that pass through the center of mass of the object as well as other axes that do not.
Index
History
The concept of moment of inertia was first introduced by the polymath Christiaan Huygens during his study of a compound pendulum.
The parallel axis theorem is also known as the Huygens–Steiner theorem, named after Christiaan Huygens and Jakob Steiner.
The perpendicular axis theorem is also known as the plane-figure theorem, as it is limited to a planar lamina (i.e., a 2D plane).
The Theorems Explained
The parallel axis theorem is used to find the moment of inertia of a rigid body about an axis that is parallel to a centre of mass axis (about which the moment of inertia is known).
The perpendicular axis theorem states that the moment of inertia of a rigid body about an axis that is mutually perpendicular to two other axes about which its moment of inertia is known is simply the sum of the moments of inertia of the rigid body about the 2 known axes.
The theorems are further explained and proved below.
The Parallel Axis Theorem
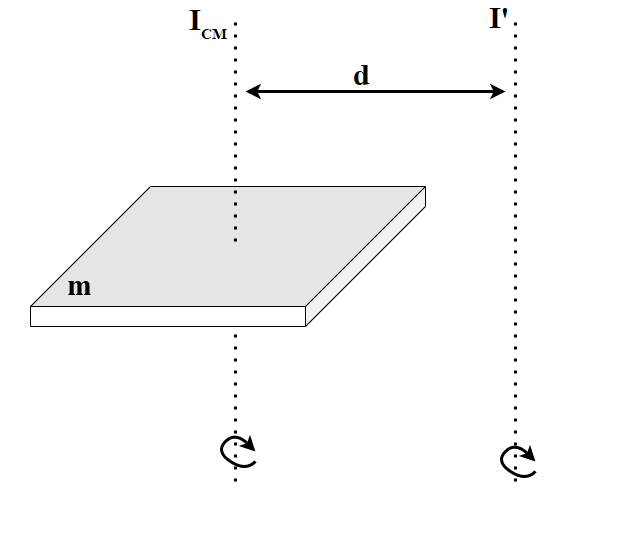
The moment of inertia of the rigid body (of mass m, as shown in Figure 1) about an axis passing through its center of mass is given as \(I_{CM}\). The parallel axis theorem states that the moment of inertia \(I^{‘}\) of the rigid body about another parallel axis (as shown) is given by:
\( I^{‘} = I_{CM} + md^{2} \)Where d is the shortest distance between the two parallel axes. This is the parallel axis theorem formula.
Proof
Let us derive the parallel axis theorem for a general rigid body as shown (Figure 2).
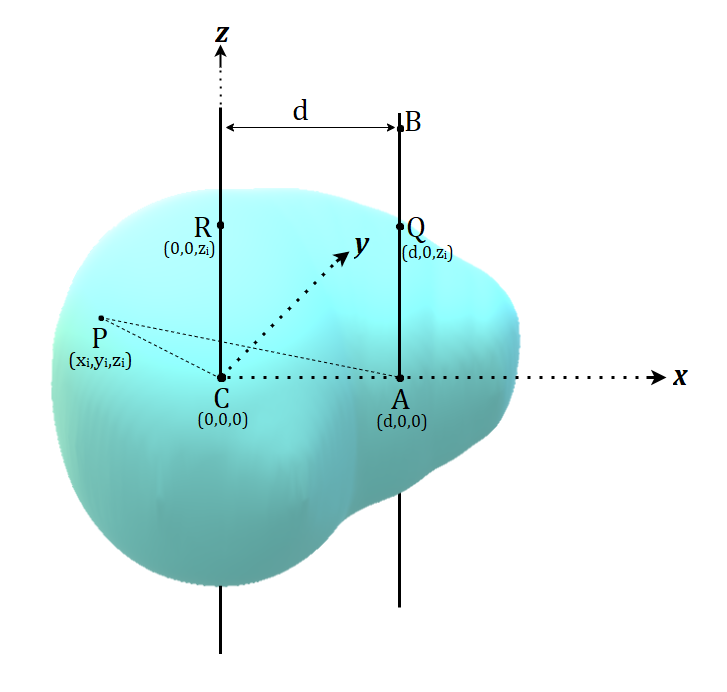
In the given figure, let the center of mass of the rigid body be at point C, which is marked as the origin of the coordinate system.
Let the moment of inertia of the body about the z-axis(CR) be \(I_{\sigma}\)
Suppose the parallel axis that we want to find the moment of inertia I’ for is the axis through AB, which is at a distance of d units from the CR axis.
Let P be an arbitrary point of the rigid body (assumed to be coplanar with the points R and Q), with mass mi and coordinates (xi , yi , zi), as shown in the figure. Let us find the moment of inertia of point P with respect to the AB axis.
Using the definition of moment of inertia:
\(I^{‘} = \sum_{i}m_i(PQ)^2\) \(I^{‘} = \sum_{i}m_i(\sqrt{(x_i – d)^2 + (y_i – 0)^2 + (z_i – z_i)^2})^2\) \(I^{‘} = \sum_{i}m_i(x_{i}^2 + y_{i}^2 + d^2 – 2x_id)\) \(I^{‘} = \sum_{i}m_i(x_{i}^2 + y_{i}^2) + \sum_{i}m_id^2 – 2d\sum_{i}m_ix_i … (1)\)Using the definition of center of mass:
\(x_{CM} = \frac{\sum_{i}m_ix_i}{\sum_{i}m_i} = 0\)(\(x_{CM} = 0\) since the center of mass is at the origin)
\(\sum_{i}m_ix_i = 0 … (2)\)The moment of inertia of point mass P about the center of mass axis CR is:
\(I_{CM} = \sum_{i}m_i(PR)^2\) \(I_{CM} = \sum_{i}m_i((x_i – 0)^2 + (y_i – 0)^2 + (z_i – z_i)^2)\) \(I_{CM} = \sum_{i}m_i(x_{i}^2 + y_{i}^2) … (3)\)Using the results from (2) and (3) in (1):
\(I^{‘} = I_{CM} + \sum_{i}m_id^2\) \(I^{‘} = I_{CM} + md^2\)This is the desired result, the parallel axis theorem formula.
The Perpendicular Axis Theorem
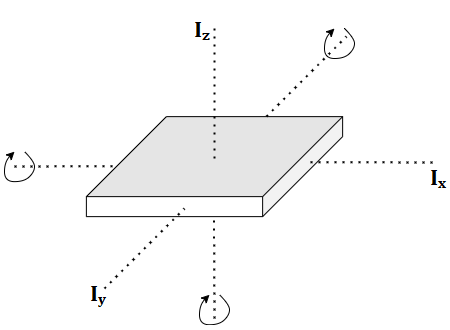
The perpendicular axis theorem states that the moment of inertia of a rigid body about an axis is the sum of the moments of inertia of the same body about 2 other mutually perpendicular axes.
Consider the rigid body shown in Figure 3. The moment of inertia of this body about the z-axis (denoted by \(I_z\)), is the sum of moments of inertia of the object about the x and the y-axes (denoted by \(I_x\) and \(I_y\)respectively).
\( I_z = I_x + I_y \)This is the perpendicular axis theorem formula.
Proof
Let us derive the perpendicular axis theorem for a general rigid body as shown (Figure 4).
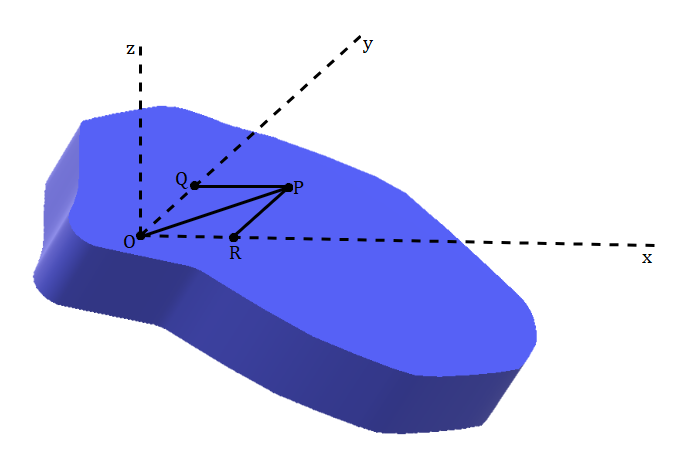
As noted earlier, the perpendicular axis theorem is only applicable to planar bodies. Let the x, y and z axes (as shown in the figure) be the 3 mutually perpendicular axes about which the moments of inertia are measured.
Consider any arbitrary point P on the rigid body. Let PR and PQ be the perpendiculars drawn from P to the x and the y axes respectively. Similarly, PO is the perpendicular drawn from P to the z-axis, where O is the origin.
Now, using the definition of moment of inertia for Iz :
\(I_z = \sum_{i}m_i(PO)^2\) \(I_z = \sum_{i}m_i(\sqrt{{PR}^2 + {RO}^2})^2\) \(I_z = \sum_{i}m_i({PR}^2 + {RO}^2)\) \(I_z = \sum_{i}m_i({PR}^2 + {PQ}^2)\) \(I_z = \sum_{i}m_i(PR)^2 + \sum_{i}m_i(PQ)^2\)These terms are simply the moments of inertia of the body about the x and y axes respectively. Therefore, we arrive at:
\( I_z = I_x + I_y \)This is the desired perpendicular axis theorem formula.
Applications
Parallel and perpendicular axis theorems are used in conjunction to find the moment of inertia of a given rigid body about any axis.
Parallel and perpendicular axis theorems can be used to find the moment of inertia of any object that is in rotational motion. Therefore, they find applications in several aspects of engineering.
Examples
Let us first take a look at a parallel axis theorem example.
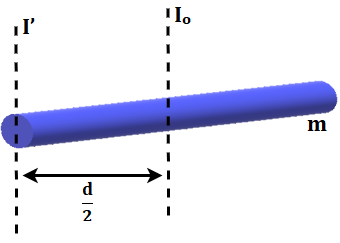
Consider the rod shown in Figure 5, with mass m and total length d units. The moment of inertia of this rod about its centre of mass, Io is:
\(I_0 = \frac{1}{12}md^2\)In order to find its moment of inertia I’ about an axis parallel to the previous axis and passing through one of its ends, we can use the parallel axis theorem.
\(I^{‘} = I_{CM} + md^2\)For the above example, we have \(I_{CM} = I_0\) and d should be replaced by \(\frac{d}{2}\).
\(I^{‘} = I_0 + m(\frac{d}{2})^2\) \(I^{‘} = \frac{md^2}{12} + \frac{md^2}{4}\) \(I^{‘} = \frac{md^2}{3}\)Let us now take a look at a perpendicular axis theorem example.
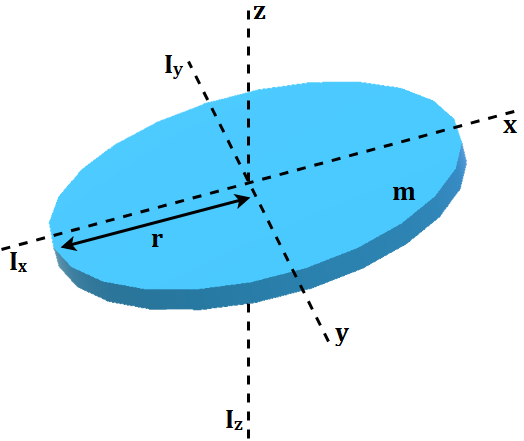
Consider the circular disc of radius r and mass m (Figure 6).
We know that the moment of inertia of this disc perpendicular to its plane and passing through its centre (Iz) is given by
\(I_z = \frac{1}{2}mr^2\)Let us use the perpendicular axis theorem to find the moments of inertia of this disc about the x and y axis (Ix and Iy respectively), when the origin is considered to be at its centre.
Since this is a symmetrical body, Ix and Iy are equal.
\(I_x = I_y = I\)From the perpendicular axis theorem:
\(I_z = I_x + I_y\)Using the above expressions:
\(\frac{1}{2}mr^2 = I + I\) \(I = \frac{1}{4}mr^2 = I_x = I_y\)FAQs
Moment of inertia (I) is a measure of the rotational inertia of an object. It is analogous to mass, which is a measure of the translational inertia of an object. It is a product of the mass of an object and the square of the distance from the object to the rotational axis. For a large object, the point masses are summed as follows:
\(I = \sum_{i}m_ir^2\)
The parallel axis theorem is used when we know the moment of inertia of a body about one axis and it is required to find the moment of inertia about another axis that is parallel to the given axis.
The perpendicular axis theorem is used when we are given 2 perpendicular axes about which the moments of inertia of a body are known, and we have to find the moment of inertia of the body about a 3rd perpendicular axis.
That’s all about Parallel and Perpendicular Axis Theorems.
How do you feel about this article? Comment down below and let us know your thoughts.
