Complex Number

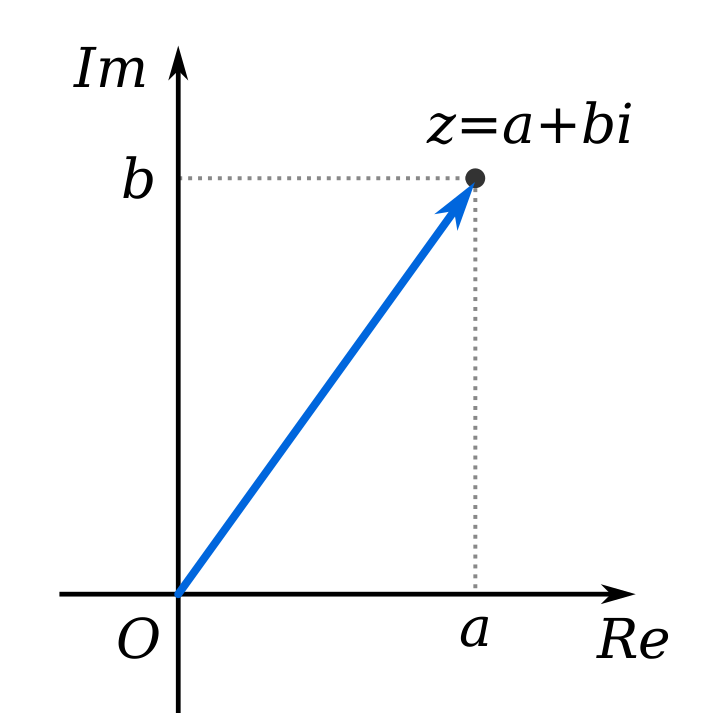
A complex number is a number that can be expressed in the form of (a+ib), where a & b are real numbers and ‘i’ is an imaginary unit i.e. i = \( \sqrt{-1}\)

Here, ‘i’ is called an imaginary number, ‘a’ is the real part of the equation and ‘b’ is the imaginary part. 

The complex no. is denoted by a symbol \(\mathbb{C}\) or C, complex numbers allow solutions to certain equations that have no real number solutions

For example, when the discriminant becomes negative in a quadratic equation. 

 i.e D= \(\sqrt{-b}\), where ‘b’ is a \(\mathbb{R}\) or Real no. 

In such situations, we can express it as D= ib.

History

The problem of complex numbers is dated back to the 1st century when Heron of Alexandria (about 75 AD) attempted to find the volume of a frustum of a pyramid, which required computing the square root of 81-144.

The quotation from Bhaskara Acharya (working in 486 AD), a Hindu mathematician: “The square of a positive number, also that of a negative number, is positive: and the square root of a positive number is two-fold, positive and negative; there is no square root of a negative number, for a negative number is not square.”

Later, around 850 AD, another Hindu mathematician, Mahavira Acharya, wrote: “As in the nature of things, a negative (quantity) is not a square (quantity), it has, therefore, no square root.” 

In the 16th-century an Italian scientist Gerolamo Cardano was attributable for introducing complex numbers, he tried to seek out solutions to cubic equations.

The complex number system is seen as the algebraic extension of the real numbers by an imaginary number.

Algebraic Operations

Let \(z_1 = a + ib\) and \(z_2 = c + id\)

Addition of Two Complex Numbers

\(z_1 + z_2 = (a+c) + i(b+d)\)

Properties:

\(
z_1+ z_2 = z_2 + z_1\\
(z_1 + z_2)+z_3 =z_1 + (z_2 +z_3)\\
z + 0 = z\\
\)

Difference Between Two Complex Numbers

\(z_1 – z_2 = (a-c) + i(b-d)\)

Multiplication of Two Complex Numbers

\(z_1*z_2 = (ac – bd) + i(ad + bc)\)

Properties:

\(
z_1z_2 = z_2z_1\\
(z_1z_2)z_3 = z_1(z_2z_3)\\
z*0 = 0\\
z*1 = z\\
z = a + ib, \text{ then } \frac{1}{z} = \frac{a}{a^2+b^2} + \frac{b}{a^2+b^2} \text{ (multiplicative inverse)}\\
z*\frac{1}{z} = 1\\
z_1(z_2 + z_3) = z_1z_2 + z_1z_3\\
\)

Division of Two Complex No.

\(
\frac{x}{y} = \frac{a + ib}{c + id}\\
\frac{x}{y} = \frac{(a + ib)(c – id)}{(c + id)(c – id)}\\
\frac{x}{y} = \frac{(a + ib)(c – id)}{c^2 – d^2}\\
\)

Power of Complex No.

\(
i^2 = (-1)\\
i^3 = (-1)i\\
i^4 = 1\\
i^5 = i\\
∴ i^{(4k)}=1\\
∴ i^{(4k+1)} = i\\
∴ i^{(4k+2)} = -1\\
∴ i^{(4k+3)} = -i\\
\)

Conjugates

 Let  \(z=a+ib; \overline{z}=a-ib\)

Here; \(\overline{z}\) is the conjugate of ‘z’

\(
(z)(\overline{z}) = (a + ib)(a – ib)\\
(z)(\overline{z}) = (a^2 + b^2)\\
\)

(OR) , we can say that

\(|z| = \sqrt{a^2 – b^2}\)

Polar Coordinates

We can donate the coordinates of a point in \((r, \theta)\).

\(
x = r\cos\theta; y = r\sin\theta\\
∴ z = r(\cos\theta + i\sin\theta)\\
\text{And } r = \sqrt{x^2 + y^2}.\\
\)

Square Root of a Complex No.

As real numbers have square roots, complex no. also do have. Here we will find how to reach the square root of a complex no.

We will be doing it in two ways.

Let (x, y) be variables and (a, b, c, d, e) be all constants. 

 Lets us find the \(\sqrt{a+ib}\).

1st Method

Let \(z^2 = (x + iy)^2 = (a + ib)\)

Expanding the square we get;

\((x^2 – y^2) + i(2xy) = a + ib\)

Now we can equate the Real part to Real and Imaginary to Imaginary

\(
(x^2 – y^2) = a … (1)\\
2xy = b \text{ or } xy = \frac{b}{2} … (2)\\
\)

Now consider the modulus (or) |z|;

 i.e.  \(|z| = \sqrt{a^2 + b^2} = c … (3)\)

{Here; let c be a constant that we got from |z|}

 Now solving (1) & (3) we can get the values of \(x^2 = d^2 \text{ & } y^2 = e^2\)  

(or) 

\(x = \pm{d} \text{ & } y = \pm{e}\).

{Here ‘d’ & ‘e’ are the constants we got after solving eq. (1) and (3)}

so, \(z = \pm(d+ie)\).

2nd Method

Note that; \((a \pm ib)^2 = (a^2 – b^2) \pm 2iab\)

\(∴ a \pm ib = \pm \sqrt{(a^2 – b^2) ± 2iab}\)

Substituting & solving using the completing the square method in the above equation gives answer directly.

Euler’s Form of Complex No.

This formula has been seen by many of us and now we will derive it.

\(e^{i\pi} + 1 = 0\)

For deriving it we shall use the Taylor series expansion

Here, e = Euler’s number and i  = Imaginary no. iota

Firstly we shall introduce the Taylor series expansion.

\(e^{x} = 1+ x + \frac{(x)^2}{2!} +\frac{(x)^3}{3!} +\frac{(x)^4}{4!} …\)

And so on…

Now we substitute ‘x’ with ‘ix’

\(∴  e^{ix} = 1+ ix + \frac{(ix)^2}{2!} +\frac{(ix)^3}{3!} +\frac{(ix)^4}{4!} …\)

as we know \(i^2 = -1\); so we can simplify it to

\(e^{ix} = 1+ ix – \frac{(x)^2}{2!} -\frac{(ix)^3}{3!} +\frac{(x)^4}{4!} …\)

Now we will group real and imaginary terms

\( e^{ix} = (1- \frac{(x)^2}{2!} + \frac{(x)^4}{4!}…..) +  i (x – \frac{(x)^3}{3!} +\frac{(x)^5}{5!}…\)

Now if we check the groups of the Taylor series, we can find that

\(\cos x = 1 – \frac{(x)^2}{2!} + \frac{(x)^4}{4!}…\)

\(\sin x  = x – \frac{(x)^3}{3!} + \frac{(x)^5}{5!}…\)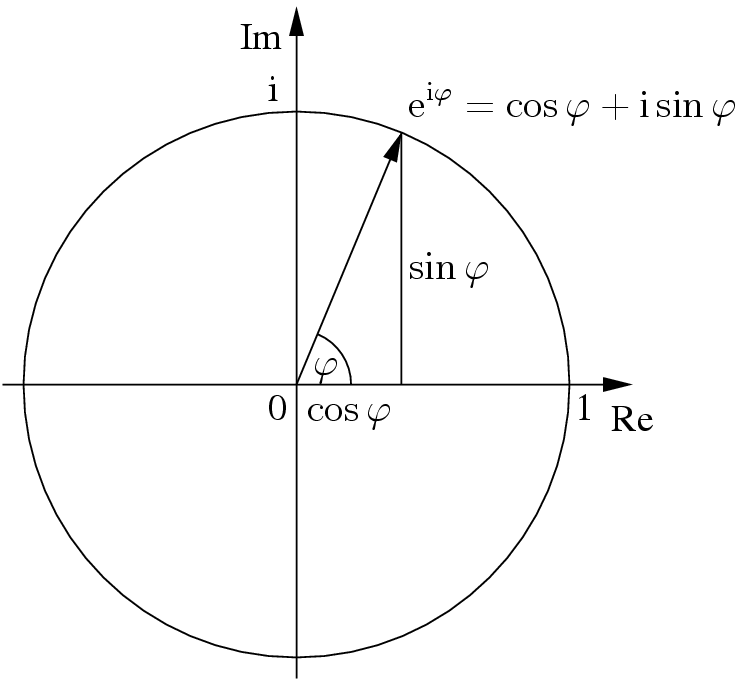

we can conclude that 

\(e^{ix} = \cos(x) + i \sin(x)\)

And this is called Euler’s Formula.

Now if we put \(x = \pi\), then we get the special case of

\(e^{i\pi} + 1 = 0\) (This is often referred as the most beautiful equation in mathematics)

Applications

• Improper Integrals – In applied fields, complex numbers are often used to compute certain real-valued improper integrals, using complex-valued functions.
• In physics, it plays an important role in many fields such as Electromagnetism, Fluid dynamics, Relativity, Quantum mechanics, etc.

As above, similarly Complex nos. can be seen working in different fields of sciences.

Examples

Question 1. Find the square root of the Complex no. 3+4i

Answer.

Method 1

Let \(z^2 = (x + iy)^2 = 24 + 10i\)

\(
∴ (x^2 – y^2) + 2ixy =24 + 10i\\
∴ (x^2 – y^2) = 24 …(1)\\
2xy = 10 \text{ (or) } xy = 5 …(2)\\
|z| = \sqrt{24^2 + 10^2}\\
(x^2 + y^2) = 26 …(3)\\
\)

From (1) and (3) we find value of \(x^2 \text{ & } y^2\)

i.e.  \(x^2 = 25  \text{ & } y^2 = 1\)

(OR) \(x = \pm{5} \text{ & } y= \pm{1}\)

so, \(z = \pm(5 + i)\)

Method 2

\((x \pm iy)^2 = (x^2 – y^2) \pm 2ixy = 24 + 10i\)

so, \(x \pm iy = \pm \sqrt{ 24 + 10i}\)

Using complete the square method

            = \(\pm \sqrt{25 + 2*5*i – 1}\)

            = \(\pm \sqrt{ 5^2 + 2*5*i + (1i)^2}\)

            = \(\pm \sqrt{(5+i)^2}\)

            = \(\pm (5+i)\).

Question 2. If \(|\frac{z – 2}{z + 2}| = \frac{\pi}{6}\), then find the locus of z.

Answer.

Let \(z = x + iy\)

\(
|\frac{x+iy-2}{x+iy+2}| = \frac{\pi}{6}\\
6|(x-2) + iy| = \pi|(x+2)+ iy|\\
\text{Squaring both sides, we get}\\
36[x^2 +4 -4x + y^2] = \pi [x^2 +4 +4x + y^2]\\
(36-\pi^2)x^2 + (36 – \pi^2)y^2 – 144 + 4\pi^2 = 0\\
\)

so, we can say that  this is a circle.

FAQs