Convex Quadrilateral

Convex Quadrilateral is one of the most commonly used shapes in many industries and fields. They are even used in astronomy. Convex quadrilaterals not only being one of the most used shapes, but are also one of the most basic shapes with four sides which enclose a space within them. 

Convex quadrilateral can be found anywhere when observed closely. For example, the building walls are convex quadrilaterals, rectangles, and even books are of the same shape.

History

The history of quadrilaterals are very old. In the age of sulbasutra the idea of a quadrilateral was limited to some regular and cyclic quadrilaterals like square, rectangle and isosceles trapezium. 

Bhaskara-I was the first one to mention a quadrilateral with unequal sides, which was later identified as a quadrilateral whose vertices lie on the circumference of a circle, which are now known as cyclic quadrilaterals. All ancient Indian scholars except Aryabhata-II only studied convex quadrilaterals.

But there are also accounts which suggest that quadrilaterals were first discovered by ancient Greeks and were first drawn by Pythagorus. 

The Shape of Convex Quadrilateral

A convex quadrilateral is a polygon with four sides and angles. The angles at vertices are all less than 180°, and their sum of 360°.

A quadrilateral is also called quadrangle, tetragon and 4-gon. Quadrilaterals vertices A, B, C and D are often represented as □ABCD.

The diagonals of a convex quadrilateral both lie and intersect inside the shape.

There are some conditions for equivalency in quadrilaterals too, similar to that of triangles. The conditions for equivalency in quadrilaterals:

1. Opposite sides must be parallel.
2. Diagonals are equal in length and perpendicularly bisect each other.

Some Common Convex Quadrilateral

Here are some common convex quadrilateral which we mostly come across in our daily life.

1. Square:  A square is usually also called a regular quadrilateral. This is because all the sides of a square are equal and all the angles are also equal, which are 90^O each. Square is also an equilateral quadrilateral.

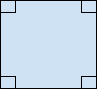
2. Rectangle: A rectangle is convex quadrilateral with all its angles as right angles and its opposite sides being equal and parallel. The diagonals of a rectangle bisect each other and are of equal length. Squares and oblongs are also rectangles.

3. Rhombus: A rhombus has all four sides of equal length with opposite sides being parallel, its opposite angles are also equal. Its diagonals perpendicularly bisect each other, but are not equal. The sum of its adjacent angles is 180°. Squares are also rhombuses but with vertices of angles 90°.

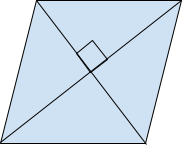
4. Parallelogram: A parallelogram is one of the most important convex quadrilaterals, its opposite sides are parallel and equal. Its opposite angles are equal, and the sum of adjacent angles is 180°. Its diagonals are not equal but they bisect each other. Rectangles are also parallelograms with angles at vertices 90°.

5. Trapezium: A trapezium is a convex quadrilateral with one pair of parallel sides. In a trapezium all sides and angles are different. 

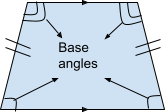
6. Isosceles Trapezium: An isosceles trapezium is, as the name suggests, is a trapezium with the two non-parallel sides as equal. In this, the base angles or the angles which are present on either side of one of the parallel sides, are equal. The sum of angles which are present between the parallel lines. is 180°. 

7. Irregular Quadrilateral: An Irregular convex quadrilateral is, as the name suggests, a quadrilateral with no two sides and angles equal. Its diagonals lie inside the area formed by its sides and the angles are all acute which make it a convex quadrilateral.

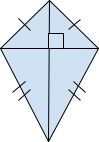
8. Kite: A kite is a convex quadrilateral which has two pairs of equal adjacent sides, and each pair is of different length. Its diagonals are not equal, but they intersect each other perpendicularly and the diagonal, on whose either side lies a pair of equal sides, is bisected by the other diagonal.

9. Cyclic Quadrilateral: Cyclic quadrilaterals are one of the most important types of convex quadrilaterals. The quadrilateral whose vertices lie on the circumference of a circle is called a cyclic quadrilateral.
One of the basic and important properties of a cyclic quadrilateral is that the sum of its opposite angles is 180°.

NOTE: Know more about Cyclic Quadrilaterals

Properties of a Convex Quadrilateral

Now, let’s move on to the discussion of properties of these quadrilateral.

Area of a Convex Quadrilateral

We are going to look at different ways we can use to find the area of convex quadrilaterals.

Using Diagonals

Here, \(p\) and \(q\) are the diagonals of a quadrilateral and \(\theta\) is the angle between them.

Bretschneider’s Formula

\(\mbox{Area } = \sqrt{(s – a)(s – b)(s – c)(s – d) – abcd [cos^2(\frac{A + C}{2})]}\)

Here, \(a\), \(b\), \(c\), and \(d\) are the sides of a quadrilateral and \(s\) is its semiperimeter and \(A\) and \(C\) are any two opposite angles.

Using Sides and Angles

\(\mbox{Area } = \frac{ad}{2} \sin A + \frac{bc}{2} \sin C\)

Here, \(a\), \(b\), \(c\), and \(d\) are the sides of a quadrilateral and \(A\) is the angle made by \(a\) and \(d\) and \(C\) is the angle made by \(b\) and \(c\).

Using Sides and Only One Angle

\(\mbox{Area } = \frac{ab}{2} \sin \alpha + \frac{\sqrt{4c^2d^2 – (c^2 + d^2 – a^2 – b^2 + 2ab \cos \alpha)}}{4}\)

Here, \(a\), \(b\), \(c\) and \(d\) are the sides of a quadrilateral and \(\alpha\) is the angle between \(a\) and \(b\).

Using Only Sides and Diagonals

\(\mbox{Area } = \sqrt{(s – a)(s – b)(s – c)(s – d) – \frac{ac + bd + pq}{4}(ac + bd – pq)}\)

Here, \(a\), \(b\), \(c\) and \(d\) are the sides of a quadrilateral and \)p\) and \(q\) are its diagonals.

Using Diagonals as Vectors

\(\mbox{Area } = \frac{|AC \times BD|}{2}\)

Here, \(AC\) and \(BD\) are the vectors of diagonals of the quadrilateral ABCD.

NOTE: Know more on Area of Quadrilateral

Lengths of Diagonals 

The lengths of diagonals of a convex quadrilateral can be found using the cosine rule in the triangles that are formed when the diagonal is drawn.

Let the diagonals of a quadrilateral be \(p\) and \(q\). Then,

\(p = \sqrt{a^2 + b^2 – 2ab \cos B} = \sqrt{c^2 + d^2 – 2cd \cos D}\)

\(q = \sqrt{a^2 + d^2 – 2ad \cos A} = \sqrt{b^2 + c^2 – 2bc \cos C}\)

Angular Bisectors

The internal angular bisectors of a quadrilateral are either concurrent or their intersection points are concyclic and hence form a cyclic quadrilateral.

Bimedians and Varignon Parallelogram

Bimedians of a quadrilateral are the line segments joining the midpoints of its opposite sides. The point of intersection of bimedians is the centroid of the quadrilateral. 

When the midpoints of adjacent sides of a quadrilateral are connected, then the resulting quadrilateral is always a parallelogram. This parallelogram is called a Varignon parallelogram.

A Varignon parallelogram has some unique properties related to the original quadrilateral.

1. Each pair of parallel sides of a varignon parallelogram is also parallel to one of the diagonals of the quadrilateral.
2. The length of sides of a varignon parallelogram is half the length of their corresponding parallel diagonal.
3. The area of a varignon parallelogram is half the area of the original quadrilateral. This is true for both convex and concave quadrilaterals.
4. The perimeter of a varignon parallelogram is the sum of diagonals of the original quadrilateral.

Some Inequalities Related to a Quadrilateral

Consider a quadrilateral with sides \(a\), \(b\), \(c\) and \(d\) and diagonals \(p\) and \(q\).

1. Sides:
   1. \(a^2 + b^2 + c^2  \gt \frac{d^2}{3}\)
   2. \(a^4 + b^4 + c^4  \ge \frac{d^4}{27}\)

2. Area:
   1. \(A \le \frac{1}{4}(a + c)(b + d)\)
   2. \(A \le \frac{1}{4}(a^2 + b^2 + c^2 + d^2)\)
   3. \(A \le \frac{1}{4}(p^2 + q^2)\)
   4. \(A \le \frac{1}{2} \sqrt{(a^2 + c^2)(b^2 + d^2)}\)
   5. \(A \le \sqrt{(s – a)(s – b)(s – c)(s – d)}\) ; here \(s\) is the semiperimeter
   6. \(A \le \frac{1}{2} \sqrt[3]{(ab + cd)(ac + bd)(ad + bc)}\)
   7. \(A \le \frac{1}{2} pq\)

Special Points in a Quadrilateral

1. Centroid: There are 3 types of centroids in a quadrilateral based on the reference using which they are formed.
   1. Vertex Centroid: It is the point of intersection of medians of a quadrilateral.
   2. Area Centroid: It is the point of intersection of line segments joining the centroids of triangles formed by a diagonal.
   3. Side Centroid: It is formed by considering the side of a quadrilateral that has constant mass per unit length.
2. Quasi-Circumcentre: The circumcentre of a quadrilateral is called a quasi-circumcentre as there are no natural analogies to the circumcentre of a quadrilateral. It is the point of intersection of line segments joining the circumcenters of triangles formed by a diagonal.
3. Quasi-Orthocentre: the orthocentre of a quadrilateral is called a quasi-orthocentre as there are no natural analogies to the orthocentre of a quadrilateral. It is the point of intersection of line segments joining the orthocenters of triangles formed by a diagonal.
4. The Quasi-Orthocentre(H), Area Centroid(G), and Quasi-Circumcentre(O) are collinear, and have the relation,
   \(HG = 2GO\)
5. Miquel point: If we consider a quadrilateral ABCD, and P and Q the points of intersection of the lines AD and BC and AB and CD respectively. Then the point through which the circles (PAB), (PCD), (QAD) and (QBC) pass through is the Miquel point.

Special Lines in a Quadrilateral

1. Newton Line: It is the line segment connecting the midpoints of diagonals. This line is bisected by the vertex centroid. 
2. The line connecting the point of intersection of diagonals and the vertex centroid, it also contains the area centroid. This line is divided by the vertex centroid in the ratio 3:1.

Applications of Convex Quadrilateral

Quadrilaterals are used in a wide range of fields from art and design to space and astronomy. Some of their uses are:

1. The properties of quadrilaterals are used in drawing floor plans of buildings.
2. Even Leonardo Da Vinci used quadrilaterals in his drawings, he used the properties of quadrilaterals in the famous painting Monalisa.
3. They are used in jewelry to make them more shiny.
4. Ptolemy used his theorem, relating the sides and diagonals of a cyclic quadrilateral, to create a trigonometric table that he applied to astronomy.

Example Problems

Question 1. Find the area of a quadrilateral whose side lengths are 2cm, 4cm, 5cm and 9cm for a, b, c, and d sides respectively, and the angle between a and d is 60°, and between b and c is 30°. Find the area of the quadrilateral.

Solution. Given, lengths and angles of the quadrilateral,
\(a\) = 2cm
\(b\) = 4cm
\(c\) = 5cm
\(d\) = 9cm
\(A\) = 60°
\(C\) = 30°

We can find the area of the given quadrilateral using the following formula,

\(\mbox{Area } = \frac{ad}{2} \sin A + \frac{bc}{2} \sin C\)

\(\mbox{Area } = \frac{2*9}{2} \sin 60° + \frac{4*5}{2} \sin 30°\)

\(\mbox{Area } = 9 * \frac{\sqrt{3}}{2} + 10 * \frac{1}{2} = 7.79 + 5\)

\(\mbox{Area } = 12.79  cm^2\).

Question 2. What is the maximum area of a quadrilateral whose side lengths are 2cm, 5cm, 7cm and 3cm for a, b, c, and d sides of the quadrilateral respectively?

Solution. Given, side lengths of the quadrilateral are,
\(a\) = 2cm
\(b\) = 5cm
\(c\) = 7cm
\(d\) = 3cm

We can find the maximum area of this quadrilateral using the following formula,

\(\mbox{Area } \le frac{1}{4} (a + c)(b + d)\)

\(\mbox{Area } \le frac{1}{4} (2 + 7)(5 + 3)\)

\(\mbox{Area } \le frac{1}{4} 9 * 8\)

\(\mbox{Area } \le 18 cm^2\)

The maximum area of quadrilaterals with these side lengths is 18 cm².

FAQs