Cyclic quadrilaterals (In Euclidean geometry) are closed quadrilateral whose all vertices lie on a single circle. This circle is called the circumscribed circle or circumcircle, and the vertices are said to be concyclic.
The center of the circle is called the circumcenter and its radius is known as the circumradius.
Index
Definition
A quadrilateral that is circumscribed in a circle is called a cyclic quadrilateral, i.e. all the four vertices of quadrilateral lie in the circumference of the circle.
More about Cyclic Quadrilaterals
Now, let us know more about cyclic quadrilaterals and their properties.
Angles
Let \(\angle{A}, \angle{B}, \angle{C} \mbox{ and } \angle{D}\) be the four angles of an inscribed quadrilateral. Then, the sum of the opposite angles is supplementary. i.e.,
\(\angle{A} + \angle{C} = 180^{\circ}\)
\(\angle{B} + \angle{D} = 180^{\circ}\)
Since it is a quadrilateral by adding all angle we get
\(\angle{A} + \angle{B} + \angle{C} + \angle{D} = 360^{\circ}\)
Let \(a, b, c \mbox{ & } d\) be the four sides of the quardilateral.
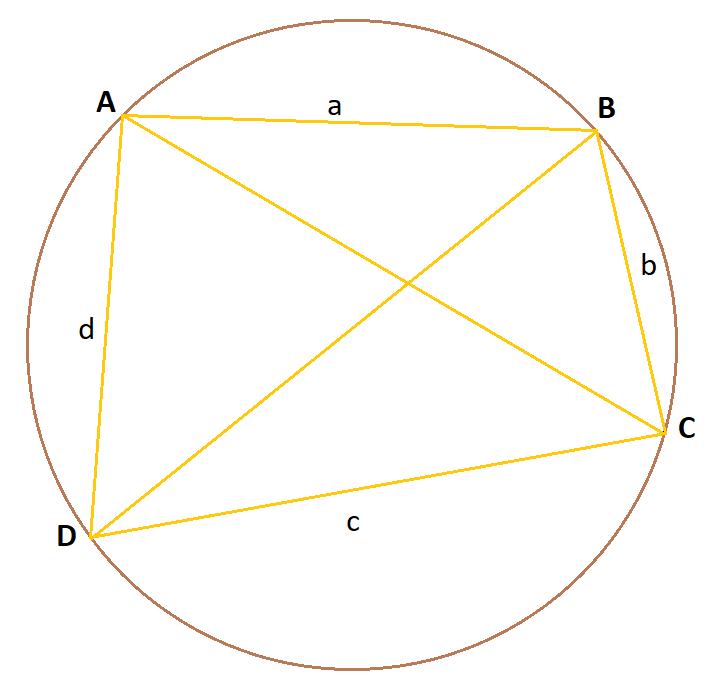
Then we can reach to the following trignometric formulas,
\(cos A = \frac{a^2 + d^2 – b^2 – c^2}{2(ad + bc)}\)
\(sin A = \frac{2\sqrt{(s-a)(s-b)(s-c)(s-d)}}{ad + bc}\)
\(tan \frac{A}{2} = \sqrt{\frac{(s-b)(s-c)}{(s-a)(s-d)}}\)
Diagonals
As we know, sides can also be written as
\(a\) = AB
\(b\) = BC
\(c\) = CD
\(d\) = DA
and, let the length of diagonals be \(d_1\) = AC and \(d_2\) = BD.
Then we can express the diagonals as
\(d_1 = \sqrt{\frac{(ac + bd)(ad + bc)}{ab + cd}}\), and
\(d_2 = \sqrt{\frac{(ac + bd)(ab + cd}{ad + bc}}\)
Area
The area(A) of cyclic quardilateral with sides \(a, b, c \mbox{ & } d\), and \(s\) being the semi-perimeter. I.e. \(s = \frac{1}{2}(a + b + c + d)\)
Hence, by Brahmagupta’s formula
\(A = \sqrt{(s-a)(s-b)(s-c)(s-d)}\)
A corollary of Bretschneider’s formula for the general quadrilateral since opposite angles are supplementary in the cyclic case.
If \(d = 0\), the cyclic quadrilateral becomes a triangle, the formula is reduced to Heron’s formula.
Note: Know more about Area of Quadrilateral.
Radius
Let \(R\) be the radius, then
\(R = \frac{1}{4}\sqrt{\frac{(ab + cd)(ac + bd)(ad + bc)}{(s – a)(s – b)(s – c)(s – d)}}\)
Theorem on Cyclic Quadrilaterals
State: The sum of either pair of opposite angles, in a cyclic quadrilateral are supplementary.
Proof: Given, A cyclic quadrilateral ABCD inscribed in a circle with center O.
Construction: Vertices A and C are joined at center O.
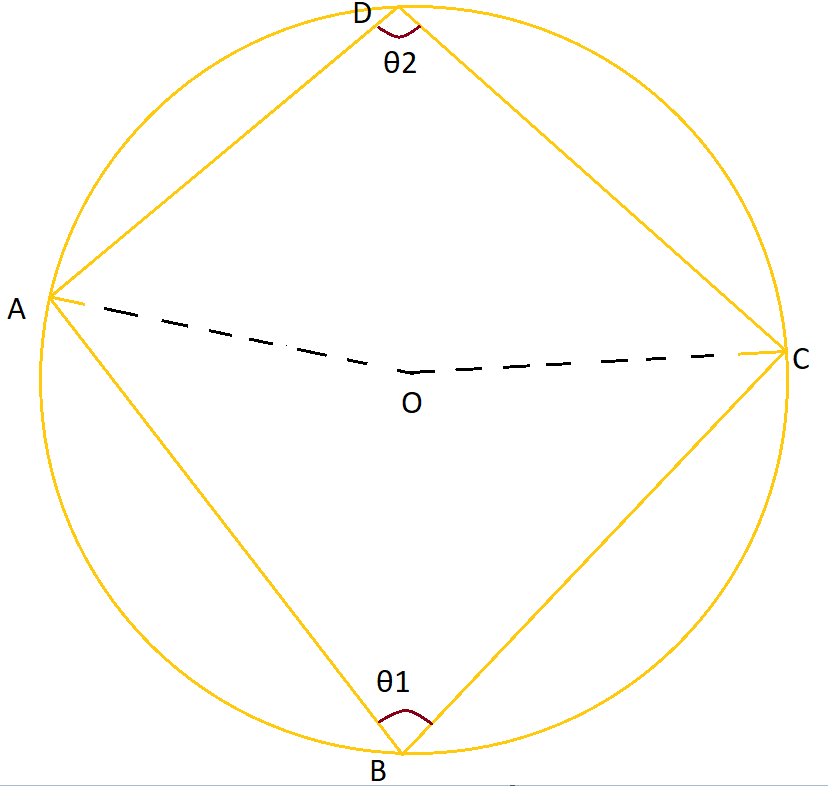
Consider arc ABC,
\(\angle AOC = 2 \angle \theta_1 \mbox{ (or) } 2\angle ABC … (1)\)
(Since, angle subtended by the arc at the centre is the double the angle subtended by it at any point of the remaining part of the circle)
Consider arc ADC,
Reflex \(\angle\)AOC = \(2\angle \theta_2 \mbox{ (or) } 2 \angle ADC … (2)\)
(Since, angle subtended by the arc at the centre is the double the angle subtended by it at any point of the remaining part of the circle)
From (1) & (2), we can say that,
\(\angle AOC + \mbox{ reflex } \angle AOC = 360^{\circ}\)
\(\Rightarrow 2 \angle ABC + 2 \angle ADC = 360^{\circ}\)
\(\Rightarrow 2\theta_1 + 2\theta_2 = 360^{\circ}\)
\(\Rightarrow \theta_1 + \theta_2 = 180^{\circ}\)
The converse of this theorem also stands true,
i.e. if the opposite angles of a given quadrilateral are supplementary, then the given quadrilateral is cyclic.
Relation Between Sides and Diagonals
Let PQ, QR, RS & SP be the four sides of the quadrilateral & \(d_1\) & \(d_2\) be the diagonals.
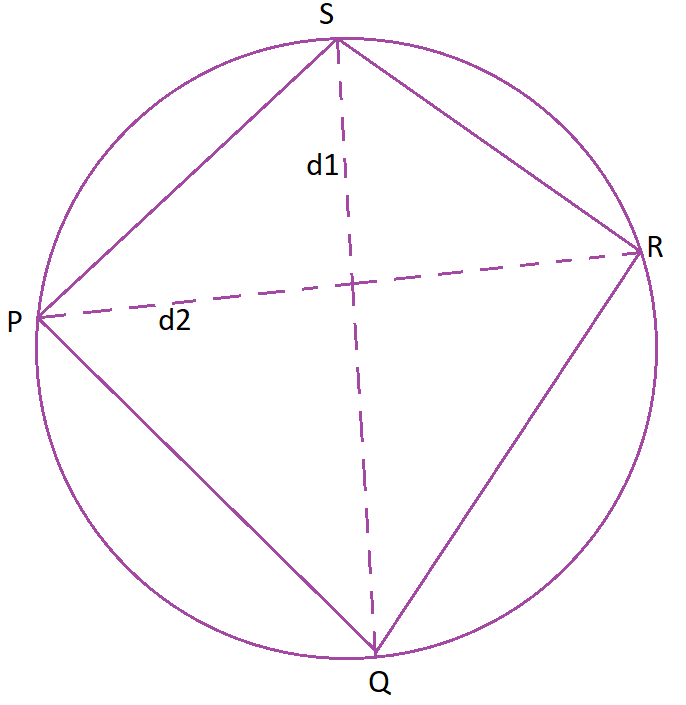
If a quadrilateral is inscribed in a circle,
then the product of the diagonals is equal to the sum of the product of its two pairs of opposite sides.
i.e.
If PQRS is a cyclic quadrilateral,
PQ and RS, and QR and PS are opposite sides,
PR(\(d_2\)) and QS(\(d_1\)) are the diagonals.
Then we can say that
(PQ x RS) + ( QR x PS) = PR x QS = \(d_1 x d_2\)
Properties of Cyclic Quadrilaterals
- The sum of the opposite pair of angles is supplementary.
- Angles to side formula
- \(cos A = \frac{a^2 + d^2 – b^2 – c^2}{2(ad + bc)}\)
- \(sin A = \frac{2\sqrt{(s-a)(s-b)(s-c)(s-d)}}{ad + bc}\)
- \(tan \frac{A}{2} = \sqrt{\frac{(s-b)(s-c)}{(s-a)(s-d)}}\)
Here, a, b, c & d are the four sides, & A, B, C & D are the four angles of the cyclic quadrillateral.
- The area of a cyclic quadrilateral is given by,
Area, \(A = \sqrt{(s-a)(s-b)(s-c)(s-d)}\)
Here, \(s\) is the semi perimeter, i.e. \(s = \frac{a + b + c + d}{2}\) - Diagonals of a quadrilateral can be expressed as
- \(d_1 = \sqrt{\frac{(ac + bd)(ad + bc)}{ab + cd}}\)
- \(d_2 = \sqrt{\frac{(ac + bd)(ab + cd}{ad + bc}}\)
Here, \(d_1 \mbox{ & } d_2\) are the two diagonals of the quadrilateral.
- All four vertices of a cyclic quadrilateral lie on the circumference of the circle.
- If ABCD is a cyclic quadrilateral, then ∠DAC = ∠DBC, ∠BAC = ∠BDC, ∠ABD = ∠ACD, ∠BCA = ∠BDA.
(Since, angles subtended by an arc at any point of the circle are equal) - If T is the point of intersection of the two diagonals, AT x TC = BT x TD.
- The exterior angle formed by any one side of the cyclic quadrilateral produced is equal to the interior angle opposite to it.
- In a given cyclic quadrilateral, \(d_1 / d_2\) = the sum of the product of opposite sides, which shares the diagonals endpoints.
- In a cyclic quadrilateral, all perpendicular bisectors from the four sides meet at the center O.
Examples on Cyclic Quadrilaterals
Question 1. If ABCD is a cyclic quadrilateral, \(\angle C = 110^{\circ}\), Then find the rest of the angles.
Solution. If \(\angle C = 110^{\circ}\),
Then, \(\angle A = 110^{\circ}\),
(Since opposite angles in a cyclic quadrilateral are equal)
Now, as we know \(\angle B = \angle D\), and total sum of all interior angles is \(360^{circ}\).
Hence, we can say that,
\(\angle A + \angle B + \angle C + \angle D = 360^{\circ}\)
\(220^{\circ} + 2 \angle D = 360^{\circ}\)
\(\angle D = 70^{\circ}\)
Therefore,
\(\angle A = 110^{\circ}\)
\(\angle B = 70^{\circ}\)
\(\angle C = 110^{\circ}\)
\(\angle D = 70^{\circ}\)
Question 2. Find the value of \(\angle PQS\) in the given figure, with O as the centre of the circle:
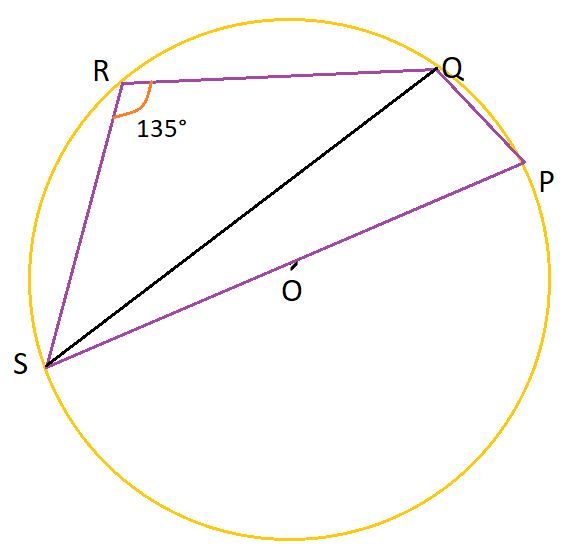
Solution. As we know, Angle subtended by the arc at the centre is the double the angle subtended by it at any point of the remaining part of the circle.
Therefore, can conclude that \(\angle PQS = 90^{\circ}\)
{SP is the diameter}
FAQs
A cyclic quadrilateral(In Euclidean geometry) is a closed quadrilateral whose all vertices lie on a single circle. This circle is called the circumscribed or circumcircle circle, and the vertices are said to be concyclic.
Opposite sides of Cyclic quadrilateral may(special case i.e. if angle is \(90^{\circ}\) or may not be equal. But the opposite sides always add on to make and supplementary angle(\(180^{\circ}\)).
As we know, all rectangles and squares are parellogram.Hence, rectangles and squares are cyclic, apart from these two cases of parellogram rest are not cyclic.
