Concave Quadrilateral

Basic Math, Maths / By

Concave Quadrilaterals are those with one angle greater than 180°. They also have general properties like, one of their diagonals being outside the quadrilateral. The most common example of a concave quadrilateral is the dart.

The Dart: A Concave Quadrilateral
The Dart: Colored region is the quadrilateral and the dotted line is one of its diagonals.

History

The idea of a concave quadrilateral was first proposed in the 10th century by Aryabhata – II. he mentioned these in his work the Mahasiddantah. Even mathematicians like Aryabhata and Bhaskhara who came before him only mentioned regular and cyclic quadrilaterals in their works. 

Properties of Concave Quadrilateral

  1. One of the internal angles is a reflex angle, i.e, it is between 180° and 360°.
  2. One of the diagonals lies outside the bounds of the quadrilateral.
  3. The sum of internal angles is 360°, same as the convex quadrilaterals.
  4. It is not possible to draw equilateral concave quadrilaterals. This is because an equilateral quadrilateral has its opposite sides parallel to each other and also its side lengths must be equal.

Applications of Concave Quadrilateral

  1. The dart shape is used in aeroplane wings and even an aeroplane itself is made in the shape of a dart.
  • The wings are at an angle to each other making them resemble the dart shape (Source).
  • F-117 Nighthawk which is a stealth attack aircraft primarily used by the USA (Source).
  1. This shape is also found in nature when moths fold their wings.
A moth when its wings are folded
A moth when its wings are folded (Source).
  1. This shape is also found in boomerangs.
A boomerang, this resembles the dart shape, a Concave Quadrilateral shape
A boomerang, this resembles the dart shape (Source).

Example Problems

Question 1. If the internal angles of a dart are 50°, 30° and  30°, then find the fourth angle.

Solution. We know that dart is also a quadrilateral, so it must follow the rule that its sum of internal angles is 360°.

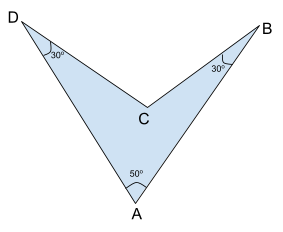
Concave Quadrilateral

From using this we can say that,

∠A + ∠B + ∠C + ∠D = 360°

50 + 30 + ∠C + 30° = 360°

∠C = 360° – 110°

∠C = 250°

Hence the reflex angle of the given dart ABCD is 250°.

Question 2. Show that the sum of internal angles of a concave quadrilateral is 360°.

Solution. We know that the sum of internal angles of any polygon can be found by using the formula,

Sum of internal angles = 180°(n – 2)
Here; ‘n’ is number of sides of the polygon

So, by substituting 4 in this formula we get the value of the sum of all internal angles of a this quadrilateral.

Sum of internal angles = 180(4 – 2) = 180(2) = 360°.

Hence, the sum of internal angles is 360°.

FAQs

What is a concave quadrilateral?

A quadrilateral one of whose angle is a reflex angle is called a concave quadrilateral.

Define a concave quadrilateral.

A concave quadrilateral is defined as, a four sided polygon with one of its angles greater than 180°, and its diagonals partially outside the bounds of the polygon.

Can an equilateral concave quadrilateral be drawn?

No, an equilateral concave quadrilateral cannot be drawn, as one of its requirements is that opposite sides must be parallel.

Are non-convex and concave quadrilaterals the same?

No, non-convex quadrilaterals are not only concave quadrilaterals but also complex quadrilaterals which crossover on themselves.

Scroll to Top
Scroll to Top