The area of quadrilateral is generally defined as the region occupied inside the boundaries of a quadrilateral or a flat object or figure.
The area is measured in square units. The standard unit is square meters (m2).
Index
About a Quadrilateral
A quadrilateral is a 4-sided polygon whose sum of interior angles is equal to 360o.
Properties of a quadrilateral are:
- 4 vertices and 4 sides.
- Sum of interior angles = 360o
- Can generally have sides of different lengths and angles of different measures.
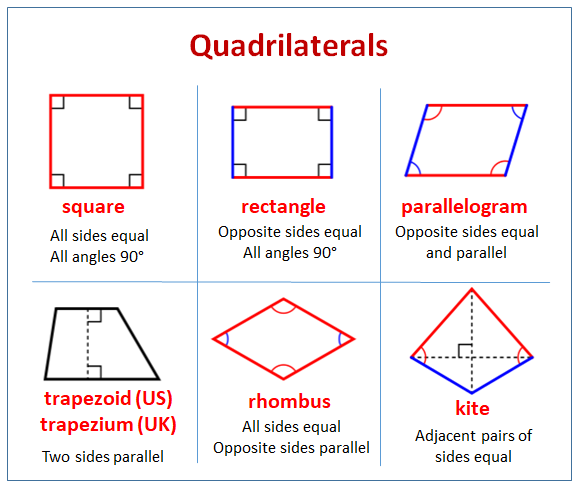
Examples of a quadrilateral are square, rectangle, parallelogram, trapezium, rhombus, and kite.
Derivation of Area of Quadrilateral
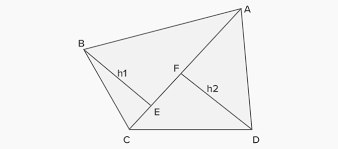
In the above quadrilateral, h1 and h2 are heights of the triangles ABC and ADC respectively. BE and DF are perpendicular to the diagonal AC.
Now,
area(quad ABCD) = area(△ABC) + area(△ADC)
area(△ABC) = \(\frac{(\mbox{base * height})}{2} = \frac{(AC*h_1)}{2}\)
area(△ADC) = \(\frac{(\mbox{base * height})}{2} = \frac{(AC*h_2)}{2}\)
⇒ area(quad ABCD) = \(\frac{(AC*h_1)}{2} + \frac{(AC*h_2)}{2} = AC \left( \frac{h_1 + h_2}{2} \right) = \frac{1}{2}*AC*(h1+h2)\)
∴ Area of Quadrilateral = \(\frac{1}{2}\) * Diagonal * Sum of Heights of Two Triangles
Areas of Different Quadrilaterals
| Quadrilaterals | Areas |
| Area of Square | (Side)2 |
| Area of rectangle | Length * breadth |
| Area of kite | \(\frac{1}{2}\) * Product of diagonals |
| Area of parallelogram | \(\mbox{base} * \mbox{height}\) |
| Area of trapezium | \(\frac{\mbox{base}_1 + \mbox{base}_2}{2} * \mbox{height}\) |
| Area of Rhombus | \(\frac{1}{2} diagonal_1 \cdot diagonal_2\) |
Solved Example
Question. In the above-given quadrilateral ABCD, what is the area of ABCD if diagonal AC = 24cm and heights are 5cm and 10cm respectively?
Solution. Given,
AC = 24cm
h1 = 5cm
h2 = 10cm
Sum of heights = 5 + 10 = 15cm
Hence area(quad ABCD) = \(\frac{1}{2}\) * Diagonal * Sum of height of two triangles
= \(\frac{1}{2} * 24 * 15 = 12 * 15 = 180cm^2\)
∴ Area of quad ABCD = 180cm2.
FAQs
Area of quadrilateral = \(\frac{1}{2}\) *Diagonal * Sum of height of two triangles
Examples of quadrilaterals are squares, rectangles, parallelograms, etc.
The area of a quadrilateral is calculated by adding the areas of the two triangles that essentially combine to give the quadrilaterals.
Read More:
1. Area of an Octagon
2. Area of a Pentagon
