Rhombus 

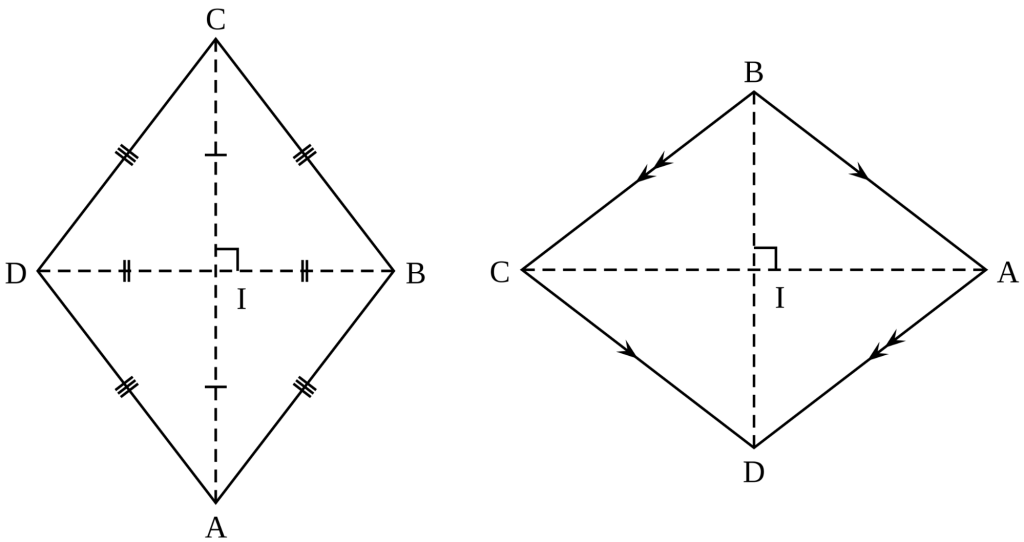
A Rhombus is a type of quadrilateral. It is a special case of a parallelogram, with its diagonals intersecting each other at 90 degrees.

It is an equilateral quadrilateral; all of its sides are equal in length, hence the term ‘rhombus’, which has been derived from the ancient Greek word ‘rhombos’, which means something that spins. 

Angles in Rhombus

1. Its shape has four interior angles.
2. The interior angles of a rhombus sum up to \(360^\circ\).
3. Opposite pair of angles are equal to each other. 
4. The adjacent angles are supplementary.
5. Diagonals bisect each other at right angles or \(90^\circ\).
6. The diagonals bisect all the four angles.

Perimeter of Rhombus

The total length of its boundaries gives the perimeter of a shape. That is the sum of all its four given sides,

The perimeter is given by \(P = 4a\), here \(P\) is the perimeter, and \(a\) is the length of each side.

Area of Rhombus

The area of the rhombus is calculated by taking the product of its diagonals and dividing it by 2,

\(A = \frac{1}{2} d_1 \cdot d_2\),

Here, \(A\) is its area & \(d_1\), and \(d_2\) are its diagonals.

Altitude of Rhombus

The height or the perpendicular distance from one of the sides from chosen base to the opposite side is the altitude. And, it is given as,

Altitude, \(H = \frac{Area}{Base}\)

Properties of a Rhombus

1. All sides are equal.
2. Opposite sides are parallel to each other.
3. Opposite angles are equal to each other.
4. Diagonals bisect each other.
5. The Sum of adjacent angles is \(180^circ\).
6. Diagonals bisect the angles at the corner.
7. It is a special case of a parallelogram, with diagonals bisecting each other at \(90^\circ\).

Solved Examples

Question 1. Find the are of a rhombus with diagonals \(d_1 = 4cm\) & \(d_2 = 10cm\).

Solution. The area of a rhombus is, 

\(A = \frac{1}{2} d_1 \cdot d_2\)

\(A = \frac{1}{2} 4 \cdot 10\)

\(A = 20 {cm}^2\)

Question 2. Find the diagonal of a rhombus if its area is 1331 cm² and length measure of longest diagonal is 22 cm.

Solution. Area can be given as,  

\(A = \frac{1}{2} d_1 \cdot d_2\)

\(1331 = \frac{1}{2}(22 \cdot d)\)

\(2662 = 22 \cdot d\)

or,  \(d = 121cm\).

Therefore, the Length of another diagonal is 121 cm.

FAQs