Area of Rhombus 

A rhombus is a type of quadrilateral. It is a special case of a parallelogram, with its diagonals intersecting each other at 90 degrees. The area of the rhombus is calculated by taking the product of its diagonals and dividing it by 2.

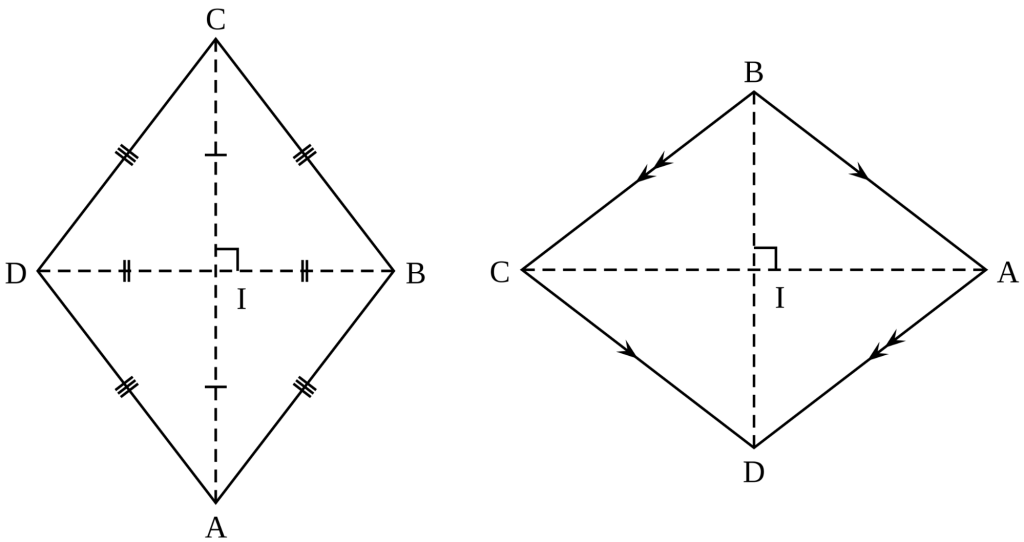
The rhombus is an equilateral quadrilateral; all of its sides are equal in length, hence the term ‘rhombus’, which has been derived from the ancient Greek word ‘rhombos’, which means something that spins. 

Area of a Rhombus

The area of the rhombus is calculated by taking the product of its diagonals and dividing it by 2, 

\(A = \frac{1}{2} d_1 \cdot d_2\),

Here, \(A\) is the area of the rhombus & \(d_1\), and \(d_2\) are its diagonals.

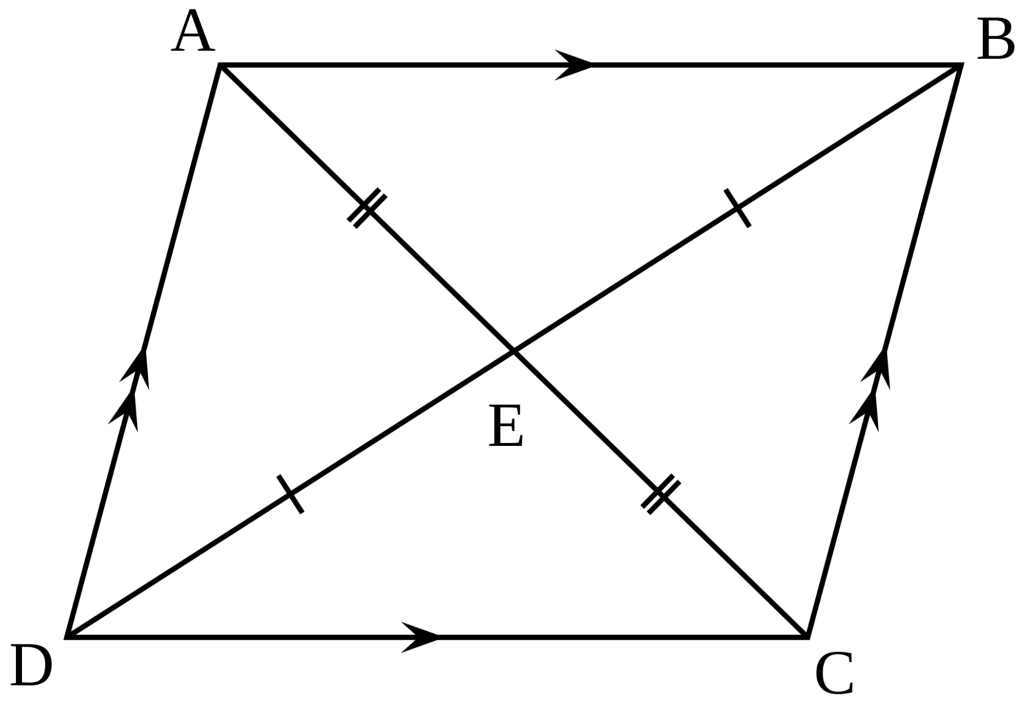
Let ABCD be a Rhombus

E being the center and AC and BD as diagonals.

The \(A\) can be written as:

\(A = 4 \cdot\) Area of \(\triangle AEB\)

\(A = 4 \cdot \frac{1}{2} (AE)(BE)\)

 (Since, diagonals perpendicularly bisect each other in a rhombus.)

\(
\begin{align}
A & = 4 \cdot \frac{1}{2} (\frac{1}{2} AC) (\frac{1}{2} BD)\\
& = 4 \cdot \frac{1}{8} AC \cdot BD\\
& = \frac{1}{2} AC \cdot BD\\
\end{align}
\)

Let \(AC = d_1\) & \(BD = d_2\)

Then, we can rewrite it as,

\(A = \frac{1}{2} d_1 \cdot d_2\)

Solved Examples

Question 1. Find the area of rhombus with the diagonals being 5cm and 10cm.

Solution. Area of a rhombus can be given as,

\(
\begin{align}
A & = \frac{1}{2} d_1 \cdot d_2\\
& = \frac{1}{2} 5 \cdot 10\\
& = 5 \cdot 5 = 25cm^2\\
\end{align}
\)

Question 2. Find the rhombus ABCD, with center O. If the area of its triangle AOB, formed by the diagonals, is 7 cm².

Solution.

Area of rhombus ABCD  = Area of \(\triangle AOB\) + Area of \(\triangle BOC\) + Area of \(\triangle COD\) + Area of \(\triangle AOD\)

\(
\begin{align}
\text{Area of rhombus ABCD}  & = 4 \cdot \text{Area of } \triangle AOB\\
& = 4 \cdot 7 = 28cm^2\\
\end{align}
\)

FAQs