Area of Octagon

The area of an octagon is a bit complex compared to lower sided shapes. Area of a regular octagon(A) = 4as. Where ‘a’ is the apothem (straight line from the centre of the pentagon to the side) and ‘s‘ is the side of the octagon.

In geometry, an octagon (from the Greek ὀκτάγωνον oktágōnon, which means “eight angles”) is an eight-sided polygon.

Sum of all the internal angles is equal to 1080?(135*8)

An octagon is a convex equilateral polygon and also a  isogonal and a isotoxal figure.

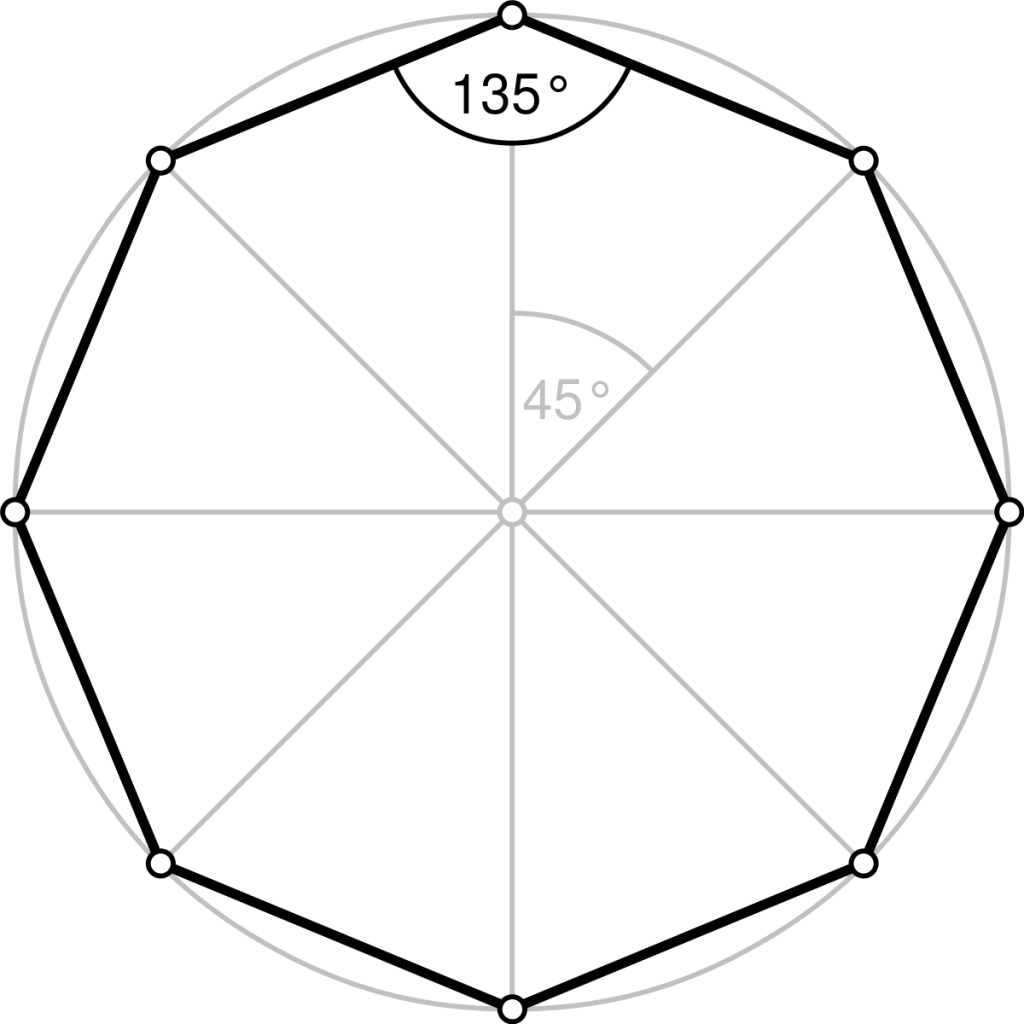
In a regular octagon each side makes an interior angle 45° at the center of octagon and the angle between two adjacent sides(exterior angle) is 135°.

Finding Area of Octagon

Octagon’s area can be found in 3 ways.

Area of Octagon from the Length of Side and Apothem

The apothem is a straight line from the centre of the pentagon to the side, intersecting the side at a 90º right angle. For octagon, apothem is its height.

Step 1: Draw five lines from the center of the pentagon to each vertex (corner).

Now we have eight equilateral triangles.

Step 2: Calculate the area of the triangle using the formula ½ bh.

Step 3: Multiply the area of 1triangle by 8 so that we can get the total octagon’s area. 

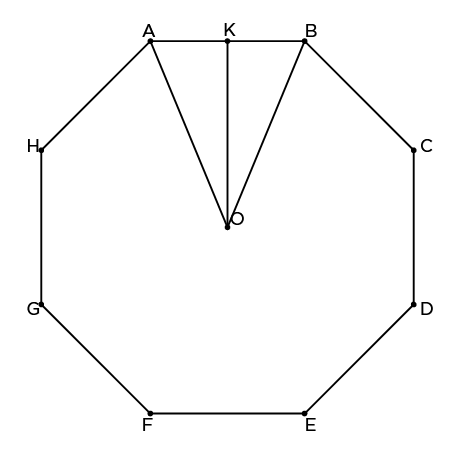
Consider a triangle AOB.

We have,
2 sin²θ = 1- cos 2θ
2 cos²θ = 1+ cos 2θ
tan²θ = (1- cos 2θ)/ (1+ cos 2θ)

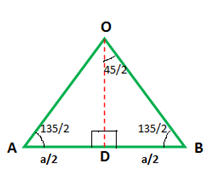
From the triangle AOB.
tan²(45/2) = (1- cos(45))/(1+cos(45))
= (1-(1/√2))/(1+(1/√2))
= (√2-1)/(√2+1)
= (√2-1)²/1

tan² (45/2) = (√2-1)²
tan(45/2)= √2-1

BD/OD = √2−1
OD = (a/2)/(√2−1) = (1+√2)a/2

Area of ∆ AOB = ½ ×AB×OD
= ½× a×(1+√2)a/2
= a²(1+√2)/4

Area of octagon = 8 × area of 1 triangle 
= 8 × a²(1+√2)/4 = 2a²(1+√2) 

Dividing into Simple Polygons

We can also find octagon’s area by dividing it into simple polygons.

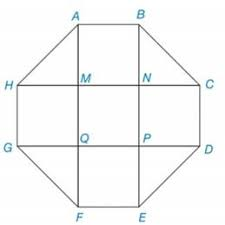
Step 1: Divide the octagon into squares and triangles.

Step 2: We end up in getting 5 squares with same side lengths and 4 triangles with same side lengths.

Step 3: Calculate the area of a square and a triangle.

Step 4: Area of the octagon = 5×area of a square + 4×area of triangle. 

Using Formula

Area of a regular polygon(A) = pa/2.

Area of a regular pentagon(A) = pa/2 = 8sa/2 = 4as.

where,
p = perimeter of the octagon,
a = apothem of the octagon,
s = side length of the octagon.

Examples

Question 1. Suraj was given an octagon of the area 68.98 units square. Help him in  finding the length of the side of the octagon.

Solution. Given that the,

Area of the octagon(A) = 68.98 units square.

We know that the` area of the octagon,

A = 2a²(1+√2)
68.98 = 2 × a²(1+√2)
a = 3.78units 

The length of the side of the octagon whose area is 68.98 units square is given by 3.78 units. 

Question 2. Perimeter of an octagonal clock is 64 cm. Find the area of the clock.

Solution. Given that the,

Perimeter of the clock = 32 cm
Perimeter of an Octagon = 8a

Where a is side of octagon 

8a = 64cm
a = 64/8 = 8 cm

Area of an Octagon = 2a²(1+√2)
Area of the clock = 2×8²(1+√2)

Area of the clock with perimeter 64 cm is 309.019cm².

Question 3. Find the apothem of the octagon whose area is 300cm².

Solution. Given that, 

Area of the octagon (A) = 300cm² 

We know that the area of octagon =  2s²(1+√2) = 4sa

Here s is side of octagon a is apothem. 

2s²(1+√2) = 300
s = 7.9
A = 4as
300 = 4 × 7.9 × a
Apothem (a)  = 9.5cm 

FAQs