Area of Pentagon

The area of a pentagon is a bit complex compared to lower sided shapes. Area of a regular pentagon = pa/2, where p = perimeter of the pentagon and a = the apothem (straight line from the centre of the pentagon to the side) of the pentagon. The area of irregular pentagon doesn’t have any formulae as such.

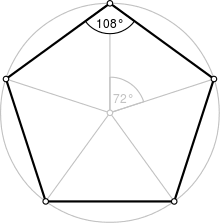
In geometry, a pentagon (from the Greek πέντε pente which means five and γωνία gonia which means angle) is a five-sided polygon.

Categories of Pentagons

In general pentagons are divided into two categories: Regular or Irregular;  Convex or Concave. 

Regular Pentagon

A regular pentagon is one with all equal sides and equal angles, with each side making an interior angle 72° at the center of pentagon and the angle between two sides (exterior angle) measuring 108°.

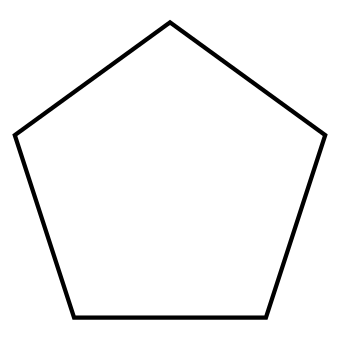
Irregular Pentagon

An irregular pentagon is a shape that does not have equal sides and/or angles and no specified angles. 

Convex Pentagon

A convex pentagon is one whose vertices / where the sides meet, is pointing outwards. All the interior angles are less than 180.

Concave Pentagon

Concave pentagon whose vertices / where the sides meet points inwards. All the angles are not less than 180.

Finding Area of Pentagon

Area of pentagon can be found in 2 ways.

Area of Pentagon from the Length of Side and Apothem

This method is for regular pentagons. Besides the side length, we need to find the “apothem” of the pentagon.

The apothem is a straight line from the centre of the pentagon to the side, intersecting the side at a 90º right angle.

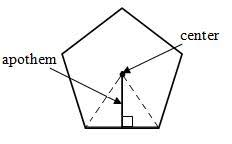
Step 1: Draw five lines from the center of the pentagon to each vertex (corners). 

Now we have five equilateral triangles.

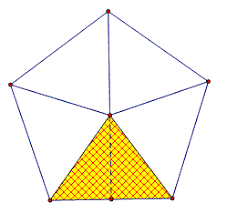
Step 2: Calculate the area of the triangle using the formula \(\).

Step 3: Multiply the area of one triangle into 5 so that we can get the total area of the pentagon.

Area of Pentagon Using Formula

Area of a regular pentagon = pa/2 = 5sa/2

where
p = the perimeter
a = the apothem
s = side length. 

Area of regular pentagon = (5s²) / (4tan(36º)) = (5s²) / (4√(5-2√5)).

Properties of Pentagon

• The sum of all the internal angles in a pentagon is 540°(108° *5) 
• A pentagon can be simple or self-intersecting.

Examples

Question 1. Find the area of the regular pentagon whose side is 14.6 cm and apothem length is 10cm.

Solution. Given that,

Side(s) = 14.6 cm
Apothem(a) = 10 cm

Area(A) = (5 ⁄ 2) × s × a
= (5 ⁄ 2) × 14.6 × 10 cm²
= 365 cm².

Question 2. Shyam was given a Pentagon of which area is 720 units square and with a side of 19 units. Help him in finding the length of the apothem of the Pentagon?

Solution. Given that,

Area of the Pentagon(A) = 720 units square.
Length of a side (s) = 19 units

We know that the area of the Pentagon(A) = 5/2 × s × a.
720 = 5/2 × 19 × a.
Apothem(a)  = 15.15 units

Therefore, the length of the apothem of the Pentagon whose are is 720 unit square is 15.15 units.

Question 3. Find the area of a pentagon of side 10 cm. 

Solution. Given side of pentagon(s) = 10 cm

Construct a triangle by joining two of the adjacent vertices with the center of a pentagon.

For pentagon height of the triangle and the apothem are same.

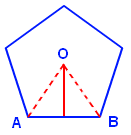
The interior angle O = 360º/5 = 72º.

Since the triangle AOB is an isosceles triangle (AO = BO).

In triangle ∆ AOB = 72º + x + x = 180º.
2x = 180º – 72º.
2x = 108º.
x = 108º/2 = 54º.

Now by using the trigonometric ratio to get the value of h.

tan A = h(½ AB)

So, h = (5) × tan 54º = 6.88.

Area of the triangle = ½ s h = ½10 ×(6.88) = 34.5 cm².

Area of polygon = 5 × Area of each triangle = 5×34.5 = 172 cm² .

Required area of the pentagon with side 10 cm is 172 cm². 

FAQs