Sierpinski Triangle

Sierpinski Triangle also called as Sierpiński Gasket or Sierpiński Sieve is a fractal with a shape of an equilateral triangle. It is subdivided recursively into smaller equilateral triangles.

This triangle is a basic example of self-similar sets i.e. it is a mathematically generated pattern that is reproducible at any magnification or reduction.

It is named after the Polish mathematician Wacław Sierpiński but it appeared as a decorative pattern several centuries before the work of Sierpiński.

History

Wacław Sierpiński described the Sierpinski triangle in 1915. But similar patterns already appeared in the 13th-century Cosmati mosaics in the cathedral of Anagni, Italy.

There are isolated triangles positioned in several churches and basilicas. They are also found on carpets in many places of central Italy, such as the Roman Basilica of Santa Maria in Cosmedin. In these cases of the isolated triangle, the iteration is at least three levels.

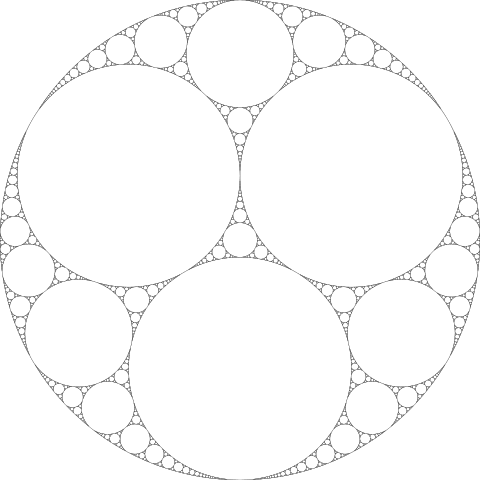
The Apollonian Gasket, shown below, which was first described as Apollonius of Perga (3rd century BC) is a curved precursor of the 20th-century Sierpiński triangle.

Construction of Sierpinski Triangle

We have various ways of constructing the Sierpiński triangle. 

Removing triangles method: The Sierpinski triangle may be formed from an equilateral triangle by repeatedly removing triangular subsets:

1. Start with an equilateral triangle.
2. Subdivide it into four smaller congruent equilateral triangles and remove the triangle at the center.
3. Repeat step 2 with each of the remaining smaller triangles infinitely.

Each removed triangle is topologically an open set. This process of recursively removing triangles is an example of a finite subdivision rule.

Similarly, we can form the Sierpinski triangle using Shrinking and duplication & Pascal’s triangle methods. 

Properties of Sierpinski Triangle

For the number of dimensions ‘d’, whenever a side of an object is doubled, 2^d copies of it are created.

i.e. for example, 
If a 1-D object has 2 copies,

then there will be 4 copies for the 2-D object,

and 8 copies for 3-D object, like a 2X2 rubik’s cube.

For the Sierpiński triangle, doubling its side creates 3 copies of itself. Thus the Sierpinski triangle has Hausdorff dimension \(d = \frac{log2}{log3} = \log_2^3 ≈ 1.585\), which follows from solving as 2^d = 3.

Sierpinski triangle’s area is zero (in Lebesgue measure). The area remaining after each iteration is \(\frac{3}{4}\) of the area from the preceding iteration and an infinite number of iterations results in an area that is approaching zero.

Examples

Question 1. Suppose a stage 0 gasket has an area of 1 square unit. One-fourth of its area is removed to make a stage 1 gasket. Find the area at stages 2, 3 & 4.

Solution. Stage = 0 => Area = 1

As we know every time the stage increases and the gasket is formed the area becomes \(\frac{3}{4}\) of the previous area.

Thus, Stage 1 area = \(\frac{3}{4}\)
Stage 2 area = \(\frac{9}{16}\)
Stage 3 area = \(\frac{27}{64}\)
and, Stage 4 area = \((\frac{3}{4})^4\)

Question 1. Find the stage of the Sierpiński Triangle if the perimeter of the triangle is \(\frac{6561}{256}\).

Solution. The perimeter of the Sierpiński Triangle is \((\frac{3^{n+1}}{2^n})\).

Here, ‘n’ = no. of stages – 1.

=> \(\frac{6561}{128} = (\frac{3^{7+1}}{2^{8}})\)

=> \(n = 7^{th} \mbox{ stage}\).

FAQs