Snell’s Law

Snell’s Law also called as Law of Refraction, is usually stated as, \(n_1 \sin \theta_1 = n_2 \sin \theta_2\), where \(\theta_1\) is angle of incidence and \(\theta_2\) is angle of  refraction and n₁, n₂ are refractive indices of the two media.

History 

Snell’s Law describing refraction was first recorded by Ptolemy in 140 A.D. It was first described by a relationship by Snellius in 1621. Willebrord Snellius (1580–1626) was a Dutch astronomer and mathematician.

Snell’s Law was explained for the first time in 1650 by Fermat’s principle of least time. This law has counterparts in other physical contexts, where electromagnetic fields exhibit similar properties.

Snell’s Law Explained

In vacuum, light travels approximately at 2.99 x 10⁸ m/s. Which is defined as c. When light propagates through various materials it will travel at a velocity v, which is less than the speed of light. 

We calculate the index of refraction(n) of the material that light is passing through by  n = c/v. Refractive indices are always greater than one. 

The degree of refraction or bending depends on the relative refractive indices of the two mediums according to a relationship called Snell’s Law.

Snell’s law states the following:

\(n_1 \sin \theta_1 = n_2 s\in \theta_2\)

Where n₁ indicates the index of refraction of the first medium
n₂ indicates the index of refraction of the second medium.
θ₁ indicates the angle of the initial beam of light with respect to the normal on the surface of the second medium
θ₂ indicates the angle of the light beam entering into the second medium. 

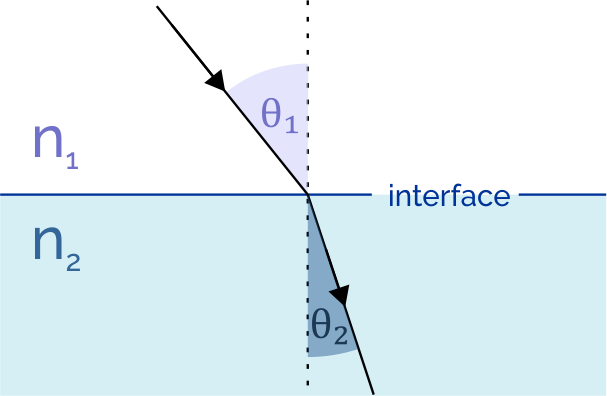
When light rays from a low index medium enter a higher index medium, the rays will bend toward the normal line on the incident surface. The opposite will occur if the rays of light go from a medium of a higher index to a lower index.

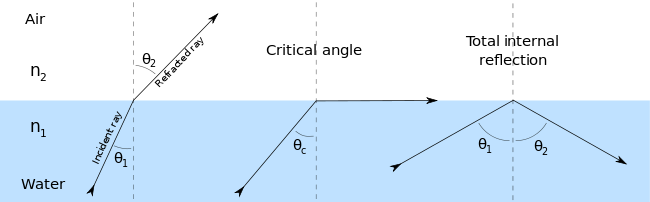
Total Internal Reflection and Critical Angle 

When a ray of light travels from denser to rarer medium, it bends away from the normal and as the angle of incidence in denser medium increases, the angle of refraction in rarer medium also increases and at a certain angle, angle of refraction becomes 90^o, this angle of incidence is called Critical Angle (θ_c).

From Snell’s law,
Sin(θ₁)/ Sin(θ₂) = n₂/n₁ 
Sin(θ_c)/ Sin(90) = n₂/n₁

Critical angle (θ_c) = arcsin(n₂/n₁)

If the angle of incidence of the light ray exceeds the critical angle then the light ray comes back into the same medium after reflection at the interface. This is called Total Internal Reflection (TIR).

Examples on Snell’s Law

Question 1. If a ray is passing from air into a medium at an angle 34° and the refractive index of the medium is 1.2, calculate the angle of incidence of the ray.

Solution. Given that n₂ = 1.2; θ₂ = 34

We know n₁ = 1

From Snell’s law, we know that 
Sin(θ₁)/ Sin(θ₂) = n₂/n₁ 
Sin(θ₁)/ Sin(34°) = 1.2/1
Sin(θ₁)= Sin(34°) × 1.2 = 0.671

θ₁ = sin^-1 (0.67)
θ₁ = 42.15°
Angle of Incidence = 42.15°.

Question 2. A cup of water is placed on a table outside in the sunlight and is filled to the top. The sun happens to be 45^o above the horizon and you notice the bottom of the cup has just become completely shaded. The cup has a depth of 15cm and you wanted to calculate the width of the bottom of the cup.  Find the width in cm.

Solution.

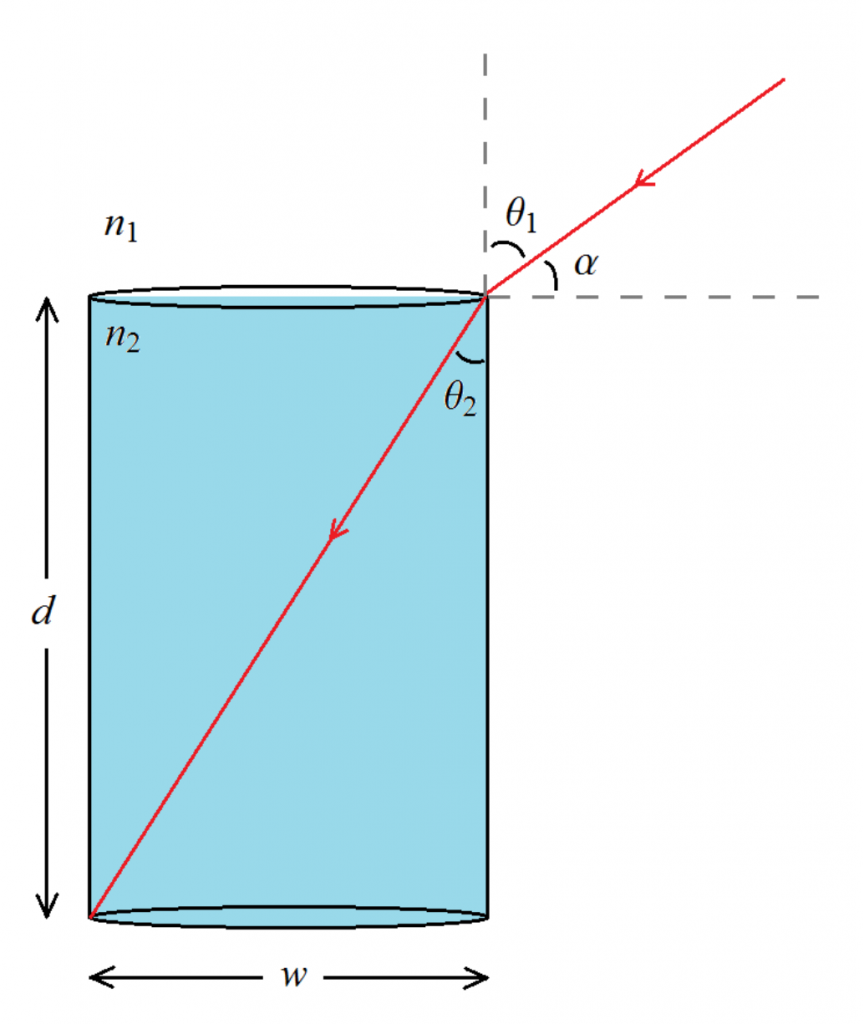
Let α be the angle w.r.t. the horizon that the sun is at i.e 45  and d is the depth of the water.

Since the light passes from air into water n₂= 1.33; n₁ = 1.

θ₁ + α = 90°
θ₁ = 90° – 45° = 45°

From Snell’s law, we know that 
Sin(θ₁)/ Sin(θ₂) = n₂/n₁ 
Sin(45°)/ Sin(θ₂) = 1.33/1
Sin(θ₂)= Sin(45°)/1.33 = 0.53 
θ₂= Sin^-1(0.53)= 32.1°

d and w forms a right angle triangle with an angle of θ2. Using the tangent 

tan(θ₂)= w/d
w = d tan(θ₂) = 15 tan(32.1°)
w  = 9.4cm

Width of the cup = 9.4cm

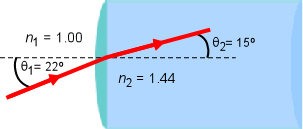
Question 3. A light travelling from air into an optical fiber which has an index of refraction of 1.44.

1. In which direction does the light bend?
2. If the angle of incidence on the end of the fiber is 22^o, what is the angle of refraction inside the fiber? 
3. Sketch the path of light as it changes media.

Solution.

1. Since the light ray  is traveling from a rarer region (air) to a denser region (fiber), it will bend toward the normal.

2. Given that θ₁ = 22^o ; n₂= 1.44; n₁= 1

From Snell’s law, we know that 
Sin(θ₁)/ Sin(θ₂) = n₂/n₁ 
Sin(22^o)/ Sin(θ₂) = 1.44/1
Sin(θ₂)= Sin(22°)/1.44 = 0.26
θ₂= Sin^-1(0.26)= 15°

The angle of refraction inside the fibre is 15°

3. The path of the light is shown in the figure below.

FAQs