Total Internal Reflection (TIR) is basically a phenomenon where light rays travel from a more optically denser medium to a less optically denser medium and gets reflected back into the more optically denser medium.
Basically, TIR happens when the angle of incidence exceeds a limiting angle known as the critical angle.
Index
Refraction at an Interface
Snell’s law tells us that light bends towards the normal when going from less optically dense to more optically dense materials and vice-versa.
At some critical angle, the transmitted beam in the less optically dense material will be at 90°.
As the angle of incidence increases, the transmitted beam angle cannot increase!
When the angle of incidence exceeds the critical angle then light ray comes back into the same medium after reflecting from the interface. This phenomenon is called Total internal reflection (TIR).
The image formed due to reflection is much brighter and the brightness is permanent.
Conditions for Total Internal Reflection
Basically, there are two main conditions for TIR to happen.
(a) The ray must travel from optically denser medium to rarer medium.
(b) The angle of incidence i must be greater than critical angle C.
| Total Internal Reflection | Reflection from a Plane Mirror |
|---|---|
| It takes place when light passes from an optically denser medium to a rarer medium when the angle of incidence is greater than the critical angle. | It takes place when light is incident on a plane mirror from any medium at any angle of incidence. |
| The entire light is reflected. | Only part of light is reflected while rest is refracted and absorbed. |
| There is no loss of energy. | The energy of the reflected ray is less than that of the incident ray. |
| The image is much brighter and the brightness is permanent. | The image is less bright and the brightness gradually decreases. |
Applications of Total Internal Reflection
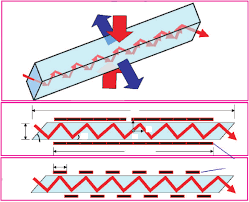
1. Zigzag Layer Slab
The circulating beam in many high-power lasers is made to zig-zag through the laser crystal to average over the thermal gradient in the crystal. Having many reflections requires the reflectivity at each interface to be high.
2. Prism
Prisms are used for reflecting beams with unit efficiency via TIR. Various configurations allow many interesting properties. Periscopes, binoculars, etc work on this principle.
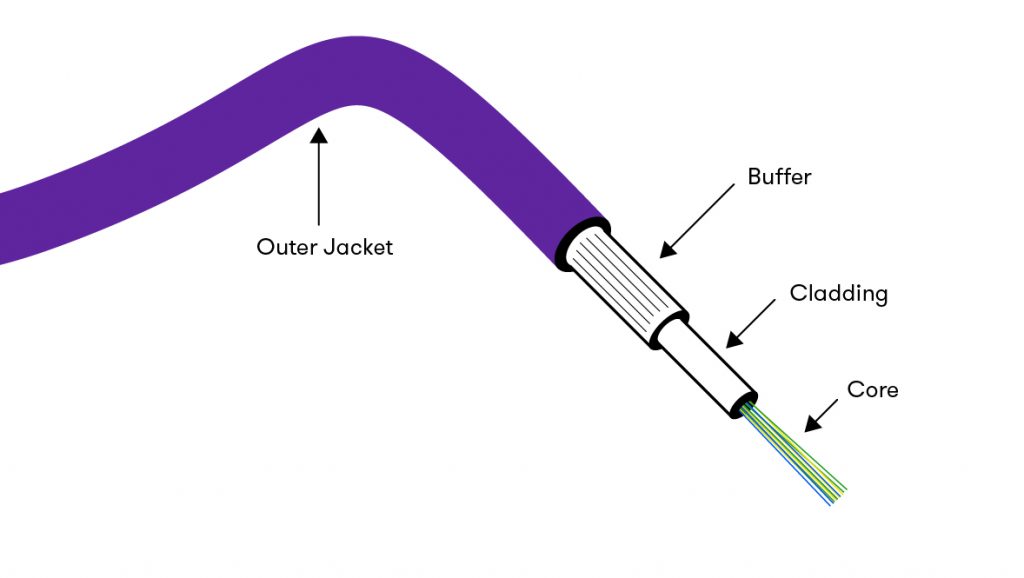
3. Fibre Optics
Glass fibers are used as waveguides to transmit light over great distance.
High index “core” guides the light.
A low index “cladding” protects the interface of the core.
The acceptance angle of a fiber determines what light will be guided through the fiber.
4. Fingerprinting
Fingertip valleys reflect light via TIR, while fingertip ridges in contact with prism frustrate the reflection.
Consequences of Total Internal Reflection
- In diamonds, the sparkling is due to the cuts of diamond faces and the High index of refraction. Incident rays can undergo multiple TIR inside a diamond before exiting the top of the diamond. This makes a diamond special than all other stones.
- Mirages
- Looming
Example
Question 1. A scuba diver is wearing a headlamp and looking up at the surface of the water. If the minimum angle to the vertical resulting in total internal reflection is 35o, what is the index of refraction of the water?
Solution. Given that n2 = 1; θ2 = 90
From Snell’s law, we know that
Sin(θ1)/ Sin(θ2) = n2/n1
Sin(35o)/ Sin(90°) = 1/n1
n1= 1/Sin(35o)
Refractive index of water is = 1.73
Question 2. A ray of light makes a transition from a sample of benzene to acetone. What is the minimum angle the light must make with respect the normal in order for the light to be completely reflected back into the sample of benzene.
The index of refraction for acetone is 1.13 and for benzene is 1.59.
Solution. Given that n2 = 1.13; θ2 = 90; n1 = 1.59
From Snell’s law, we know that
Sin(θ1)/ Sin(θ2) = n2/n1
Sin(θ1)/ Sin(90°) = 1.13/1.59 = 0.71
Sin(θ1)= Sin(90°) × 0.71
θ1 = sin-1 (0.71)
θ1 = 46°
The minimum angle the light must make with respect the normal in order for the light to be completely reflected back into the sample of benzene is 46°.
Question 3. You have a piece of optical wire with a light beam traveling through it surrounded by a liquid with an index of refraction of 1.33. If the index of refraction of the wire is 1.85, what is the critical angle needed to achieve total internal reflection?
Solution. Given that n2 = 1.33; θ2 = 90; n1 = 1.85
From Snell’s law, we know that
Sin(θ1)/ Sin(θ2) = n2/n1
Sin(θc)/ Sin(90°) = 1.53/1.85 = 0.71
θc = sin-1 (0.71)
θc = 46°
The critical angle needed for achieving TIR is 46°.
FAQs
DSLR cameras use this phenomenon.
No, dispersion of light is not associated with TIR.
The optical fibre is a device that works on the principle of total internal reflection by which light signals can be transmitted from one place to another with a negligible loss of energy.