Critical Angle

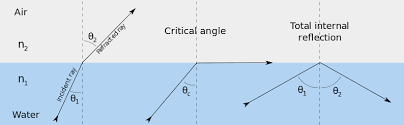
When a ray of light travels from denser to rarer medium it bends away from the normal and as the angle of incidence in denser medium increases, the angle of refraction in the rarer medium also increases and at a certain angle, the angle of refraction becomes 90^o, this angle of incidence is called critical angle (θ_c).

From Snell’s law,

Here, 
n₁ = refractive index of water 
θ₁ = angle of incidence
n₂ = refractive index of air
θ₂ = angle of refraction 

so,
• Sin(θ_c)/ Sin(90) = n₂/n₁
• Critical angle (θ_c)= arcsin(n₂/n₁)

Example:
Refraction from water to air (refractive index of water is 1.33)
θ_c = arcsin(1/1.33) = 49 degrees 

If the angle of incidence of the light ray exceeds the θ_c then the light ray comes back into the same medium after reflection at the interface. This is called Total internal reflection (TIR).

Applications

• The concept of θ_c is the basis for the construction and working of fiber optic cables.
• Fiber optics using glass or plastic are  used in telecommunications for telephone calls, video signals, and computer data. useful in medical diagnostics: colonoscopy, endoscopy, bronchoscopy.
• Working of total internal reflection fluorescence microscope.
• Multi touch screens.
• Prismatic binoculars.

Critical Angle in Diamond

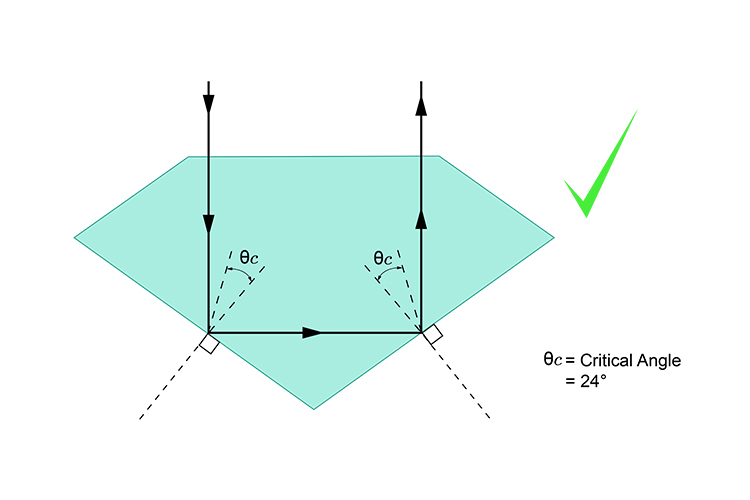
From the above equation for the critical angle.

θ_c = arcsin(n2/n1)

Refractive index of diamond is 2.42 

So,  
θ_c (Critical Angle of Diamond) = arcsin(1.000/2.42) = 24.4 degrees

Solved Examples

Question 1. Critical angle of glass is θ₁ and that of water is θ₂. The θ_c for water and glass surface would be (µ_g = 3/2, µ_w = 4/3)

1. less than θ₂
2. between  θ₁ and θ₂
3. greater than θ₂
4. less than θ₁

Solution.

sin θ₁ = 1/µ_g  and sin θ₂ = 1/µ_w

Since, µ_g > µ_w, θ₁ < θ₂

Critical angle θ between glass and water will be given by
sin θ = µ_w/µ_g
Or θ > θ2

So we conclude that option (3) is correct.

Question 2. A disc is placed on the surface of a pond. The refractive index of the pond is  5/3. A source of light is placed 4m below the surface of liquid. Find the minimum radius of the disc so that the light doesn’t come out?

Solution.  

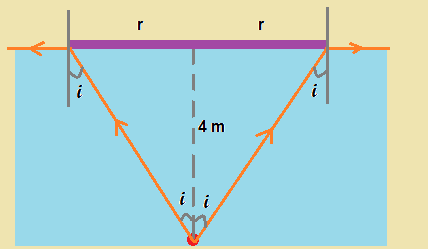
From the figure we can notice that the direction of light ray at the edge of disc is parallel to light surface, when the incident ray makes θ_c.

After the edge we can note that light rays will be reflected due to total internal reflection and the whole radiation from light source is blocked

Hence the angle ‘i’ shown in the figure should be the θ_c. 

For the θ_c we have,  

sin i = 1/μ = 3/5 
tan i = 3/4 … (1)

From the  figure, we can conclude that tan i = r/4  … (2)

hence from (1) and (2),  the required radius = 3 m

FAQs