Law of Radioactive Decay

The law of radioactive decay states that at any instant the rate of radioactive disintegration is directly proportional to the number of nuclei present in it, at that instance of time.

Radioactive decay is the process by which an unstable atomic nucleus loses its energy due to radiation. It is a random process at the level of single atoms.

History

The phenomenon of radioactivity was discovered by a French scientist, Henry Becquerel, in 1896 while working with phosphorescent materials. At first, this radiation was similar to that seen by X-rays. Further research was done by Becquerel, Ernest Rutherford, Paul Villiard, Marie Curie, and Pierre Curie.

Rutherford was the first person to realize that all such elements decay following the same mathematical formula.

Law of Radioactive Decay Explained

Statement

At any instant, the rate of radioactive disintegration is directly proportional to the number of nuclei of the radioactive element present at that instant.

Types of Radioactive Decay

There are three types of radioactive decay:

• Alpha Decay: This occurs when the nucleus of an atom ejects an alpha particle(helium nucleus).
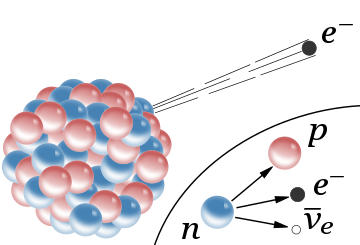
• Beta Decay:
  • Beta-minus decay:- When the nucleus emits an electron and an antineutrino in a process that changes a neutron to a proton.
  •  Beta-plus decay:- When the nucleus emits a positron and a neutrino in a process that changes a proton to a neutron.
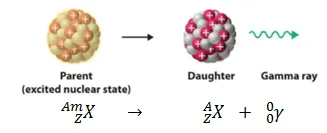
• Gamma Decay: Occurs when a radioactive nucleus first decays by the emission of an alpha or beta particle. The child nucleus is usually left in an excited state, which may again decay to a lower energy state by emitting a gamma-ray photon.

According to the quantum theory, the time at which a particular atom starts decaying is impossible to predict, no matter how long the atom has existed. However, the overall decay rate for a significant number of identical atoms can be expressed as half-life.

Half-life is the time taken for a given amount of radioactive substance to decay to half of its initial value.

The SI unit for radioactive activity is becquerel(Bq). One Bq is defined as one transformation per second.

Derivation of the Law of Radioactive Decay

When a radioactive substance undergoes \(\alpha, \beta, \gamma\) decay, the number of nuclei undergoing the decay, per unit time, is proportional to the total number of nuclei in the substance.

If \(N\) is the total number of nuclei  and \(\Delta N\) is the number of nuclei undergoing decay in time \(\Delta t\) then,

\(\frac{\Delta N}{\Delta t} \propto N\)

⇒ \(\frac{\Delta N}{\Delta t} = \lambda N\)

Where, 
\(\lambda\) – radioactive decay constant or disintegration constant

The change in the number of nuclei is \(dN\) = \(– \Delta N\) in time \(\Delta t\). Thus the rate of change of N is (in the limit \(\Delta t \rightarrow 0\))

\(\frac{dN}{dt} = -\lambda N\)

⇒ \(\frac{dN}{N}= -\lambda dt\)

Integrating on both sides,

\(\int_{N_0}^{N} \frac{dN}{N} = -\lambda \int_{t_0}^{t} dt\)

Setting \(t_0 = 0\),

⇒  \(\ln \frac{N}{N_0} = -\lambda t\)

∴  \(N(t) = N_{0} e^{-\lambda t}\) – (1) 

Decay Rate

The decay rate(\(R\)) gives the number of nuclei decaying per unit time.

\(R = -\frac{dN}{dt}\)

Differentiating eq (1) on both sides,
⇒ \(R = \lambda N_0 e^{-\lambda t}\)

This can be written as,
∴  \(R = R_0 e^{-\lambda t}\)
Where, R₀ is the radioactive decay rate at the time t = 0. It can also be written as
∴ \(R = \lambda N\)

Half-Life   

According to the definition of half-life,

\(R = (\frac{1}{2}) R_0 \mbox{ and } t = T_{\frac{1}{2}}\)

⇒ \(T_{\frac{1}{2}} = \frac{\ln(2)}{\lambda}\)

∴ \(T_{\frac{1}{2}} = 0.693 \lambda\)

Mean Life

Mean life(\(\tau\)) is the average time that an unstable particle or nucleus survives before it decays.

\(\tau = \frac{\lambda N_0 \int_0^{\infty} t e^{-\lambda dt}}{N_0}\)

⇒ \(\tau = \lambda N_0 \int^0_{\infty} t e^{-\lambda dt}\)

On solving the integral,

∴ \(\tau = \frac{1}{\lambda}\)

Example

Question. The half-life of U₉₂²³⁸ undergoing ?-decay is 4.5×10⁹ years. What is the decay rate for a 1g sample?

Solution. \(T_{\frac{1}{2}} = 4.5 * 10^9 = 4.5 * 10^9 * 10^7 = 1.42 * 10^{17} \mbox{ seconds }\)

As 1g of U₉₂²³⁸ contains \(\frac{1}{238 * 10^{-3}} * 6.025 x 10^{26} = 25.3 * 10^{20}\) atoms

\(R = \lambda N\)

⇒ \(R = (\frac{0.693}{T_{\frac{1}{2}}})N\)

    ⇒ \(R = (\frac{0.693}{1.42 * 10^{17}})25.3 * 10^{20}\)

    ∴  \(R = 1.23 * 10^4\) Bq

FAQs