The volume of the Hemisphere is an important topic and an important formula and keeps appearing in a lot of exams. To understand this properly, let us start with 3D shapes.
We know and see a lot of three-dimensional shapes in daily life. The 3D shapes have three measurements, i.e., length, breadth, and height.
We know that 3D shapes do not lie on an x-y axis. Most of the 3D objects are obtained from the rotation of the 2D objects.
The sphere is one of the best examples of a 3D body we can obtain by rotating a 2D shape, a circle.
Index
Hemisphere
A sphere is a 3D solid figure, made up of all points in space, lying at a constant distance called the radius, from a fixed central point called the centre of the sphere.
Now, if a plane cuts the sphere into two halves passing through the centre, it forms two hemispheres.
Equation of Hemisphere
With radius ‘r’ as the centre of origin, it comes out to be,
Equation of Hemisphere: x2 + y2 + z2 = r2
And the Cartesian equation is
\((x – x_0)^2 + (y – y_0)^2 + (z – z_0)^2 = r^2\)The Surface Area of a Hemisphere
Let ‘r’ be the radius of the sphere, then
The surface area of a sphere is given by \(4\pi r^2\)
And since we know that hemisphere is exactly half of the sphere hence, its surface area will be
Surface area(Hemisphere) = Surface area of half of the sphere + Area of the circle on the bottom of hemisphere
= \(2 \pi r^2 + \pi r^2\)
= \(3 \pi r^2\)
The Volume of a Hemisphere
Let ‘r’ be the radius of the sphere, then
Volume of sphere = \(\frac{4}{3} \pi r^3\)
Volume of Hemisphere Formula = \(\frac{Volume of sphere}{2}\)
=\( \frac{\frac{4}{3} \pi r^3}{2}\)
So, Volume of a hemisphere formula = \(\frac{2}{3} \pi r^3\)
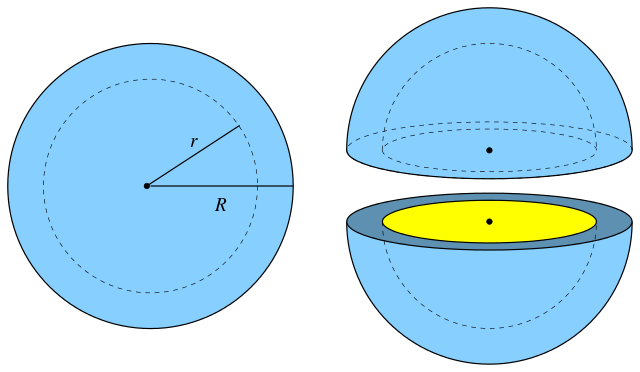
If one scoops out the inner of the hemisphere, it forms the hollow hemisphere.
The total Surface area(TSA) of the hollow hemisphere = Surface area of Hemisphere + surface area of inner surface – overlap
TSA (given R and r are outer and inner radii of the hollow hemisphere)
= \((2\pi R^2 + \pi R^2) + (2\pi r^2) – (\pi r^2)\)
= \(3\pi R^2 + \pi r^2\)
The volume of the hollow Hemisphere = Volume of the total hemisphere – Volume of the removed hemisphere
= \(\frac{2}{3} \pi R^3 – \frac{2}{3} \pi r^3\)
= \(\frac{2}{3} \pi (R^3 – r^3)\)
Problems
Q. Find the volume of the Hemisphere with a radius 3cm.
Sol. Volume = \(\frac{2}{3} \pi r^3\)
= \(\frac{2}{3} \pi (3)^3\)
= \(18\pi\)
Q. If the volume of a hemisphere is \(6174\pi\), find its radius.
Sol. Volume = \(\frac{2}{3} \pi r^3\)
=> \(6174\pi = \frac{2}{3} \pi r^3\)
Bringing 2/3 to the left
=> \(6174 \cdot \frac{3}{2} = r^3 \)
=> \(9261 = r^3 \)
We know that cube root of 9261 is 21.
Thus \( r = 21 cm \)
FAQs
When a plane cuts a sphere into two halves passing by its center, it forms two hemispheres.
Volume = \(\frac{2}{3} \pi r^3\)
Volume = \(\frac{2}{3} \pi (R^3 – r^3)\)
The surface area of the hemisphere = \(3\pi R^2\)
Similar Articles
