Ampere’s Law

Ampere’s Law is an integral part of the concept of electromagnetism and is also known as Ampère’s circuital law.

Ampère’s law is an alternative expression of Biot Savart Law.

History

The Ampere’s law was first discovered by French physicist André-Marie Ampère in 1826. This law’s final equation was derived by Scottish scientist James Clerk Maxwell in 1861.

In 1865, Maxwell generalized the equation to apply to time-varying currents by adding the displacement current term.

This modern form of the law, sometimes, is also referred to as Ampère-Maxwell law.

Ampere’s Law Explained

This law defines a relationship between the current through a closed loop and the magnetic field created around it.

Statement

Ampere’s Law Statement

“For any closed path, the line integral of the component of magnetic field tangent in the direction of the path element is equal to the permeability times the electric current enclosed in the loop.”

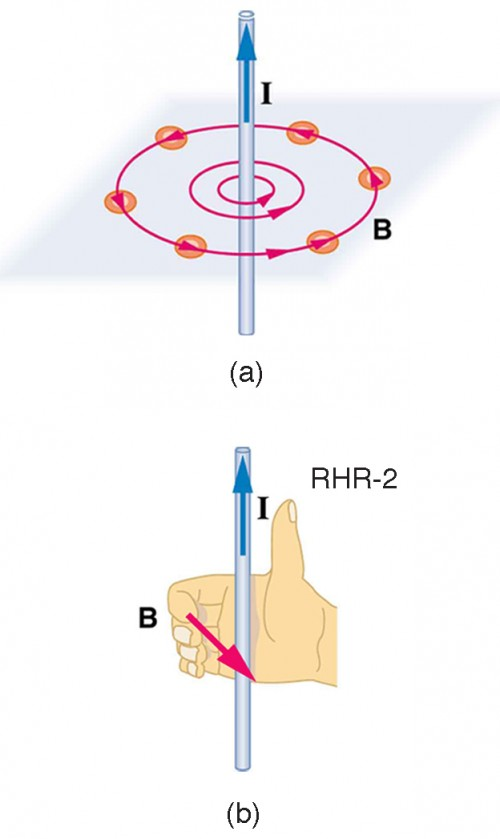
The direction of the magnetic field can be visualised using the Right-Hand Rule: Point the thumb in the direction of the current, and the fingers curl in the direction of the magnetic field loops created by it.

Equation

Where,
\(B\) – Magnetic field at position \(ds\),
\(ds\) – Component of the path length, s
\(\mu_0\) – Permeability of vacuum,
\(I\)    – Current through the closed loop

It depicts that on continuous passage of current through the closed loop, a magnetic field is created around the conductor.

From the equations we can see that:

• The total magnetic field varies, upon varying the current flowing through a closed path.
• If the magnetic field is known, the current flowing through the closed loop can be calculated by integrating the magnetic field at each point/position of the loop.
• \(\oint \overrightarrow{B}.\overrightarrow{ds} = 0\) doesn’t necessarily mean that the magnetic field is zero, but that the current flow is zero.

There are certain conditions to apply Ampere’s law:

• The current flowing through the closed loop needs to be steady.
• Only currents crossing the area inside the loop path are taken into account and have some contribution to the magnetic field.
• Currents have to be taken with their algebraic signs (those going “out” of the surface are positive, those going “in” are negative) – use the right hand’s rule to determine directions and signs.

For circular loops, \(\oint \overrightarrow{ds}\) becomes \(2\pi r\) where r is the radius of the circular loop.

Hence the equation becomes,

\(B.2 \pi r = \mu_0 I\)
\(∴ B = \frac{\mu_0 I}{2\pi r}\)

Applications of Ampere’s Law

• The main application is calculating the magnetic field generated by an electric current, which is used in electromagnets, motors, generators, transforms etc.
• It is also applied in place of Biot Savart law, since Ampere’s law simplifies calculation by using symmetry.

Ampere’s Law Examples

Question 1. Find the current in a long straight wire that would produce a magnetic field twice the strength of the Earth’s at a distance of 5.0cm from the wire.(Magnetic field of Earth = \(5.0⨯10^{-5} T\), \(\mu_0 = 4 \pi ⨯10^{-7} T m/A\))

Solution. According to the question,
B_wire = 2⨯B_earth
∴ B_wire = 10⨯10^-5 T = 1⨯10^-4 T
r = 5.0 cm

We know,
\( I = \frac{2 \pi r B}{\mu_0} = \frac{2 \pi (5.0⨯10^{-2})(1⨯10^{-1}T)}{4 \pi ⨯10^{-7}Tm/A}\)
\(∴ I = 25 A\)

Question 2. Find the magnetic flux density of a finite length conductor of radius 15cm and current 5A in air( in 10^-6 order).

Solution. Given,
I = 5 A
R = 15 cm 

As,
\(B = \frac{mu_0 I}{2 \pi r}\)
\(B = \frac{4 \pi ⨯10^{-7}⨯3}{2 \pi ⨯0.12}\)
\(∴ B = 5⨯10^{-6}T\)

FAQs