Biot Savart Law is basically an equation describing the magnetic field generated by a constant electric current.
It establishes a relationship between the magnetic field and the magnitude, direction, length, and proximity of the electric current.
Two French physicists, Jean-Baptiste Biot and Felix Savart discovered this law in 1820. Thus, the law was named after them
Index
Explanation
So, let’s have look at the explanation of this law which is another interesting topic in physics.
Before that we need to know that an electric current in a conductor produces a magnetic field.
Statement
Biot Savart Law Statement: “The law states the value of the magnetic field at a specific point in space from one short segment of a current-carrying conductor depends on each factor that influences the field.”
The value of the magnetic field at a point in the surrounding space may be considered the sum of all the contributions from each small element, or segment, of a current-carrying conductor.
Equation
Let us take a current-carrying wire I in a particular direction. Take a small element of the wire of length dl. The direction of this element is along that of the current so that it forms a vector Idl.
To know the magnetic field produced at a point due to this small element, one can apply Biot-Savart’s Law. The law is basically a line integral evaluated over the path C in which the electric currents flow (e.g. the wire).
So, let us have a look at the equation of Biot Savart Law
\(\large{B(r) = \frac{\mu_0}{4\pi}\int_c{\frac{I\, dl ⨯ r’}{{|r’|}^3}}}\)Where,
\(B(r)\) – Magnetic field at position r in 3D space,
\(I\) – Current through the conductor,
\(dl\) – vector along the path C,
\(l\) – point on path C,
\(r’\) – displacement vector from element(\(dl\)) at point \(l\) to point at which magnetic field is being computed(\(r\)).
\(\mu_0\) – Magnetic constant/ Permeability of vaccum.
The magnitude of the field is
\(\large{B(r) = \frac{\mu_0}{4\pi}\int_c{\frac{I\, dl ⨯ sin\theta}{{|r’|}^2}}}\)Where,
\(\theta\) is the angle between vectors \(dl\) and \(dr\)
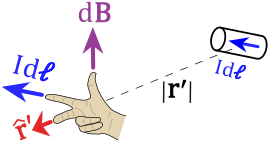
The law applies to infinitely long wires as well.
To apply the equation, the point in space where the magnetic field is to be calculated is arbitrarily chosen(r). Holding that point fixed, the line integral over the path of the electric current is calculated to find the total magnetic field at that point.
The application of this law implicitly relies on the superposition principle for magnetic fields, i.e. the fact that the magnetic field is a vector sum of the field created by each infinitesimal section of the wire individually.
The law can be applied in 2D space too. It is used when the sources are invariant in one direction. The equation would be as follows:
\(\large{B(r) = \frac{\mu_0}{2\pi}\int_c{\frac{J\, dl ⨯ r’}{|r’|}}}\)
where,
\(J\) – Current density of the current-carrying conductor.
Applications
- Used in aerodynamic theory to calculate velocity induced by vortex lines.
- Can be used to calculate the magnetic field even at atomic or molecular levels.
Example
Question. Find an expression for the magnetic field at the centre of a current-carrying circular loop.
Solution. Consider a current-carrying(I) circular loop of radius R.
At a point \(dl\) on the loop,
\(dl = R d\theta \, \hat{\theta_0}\\
dB = \frac{\mu_0}{4\pi} \, \frac{I \, dl ⨯ \hat{r}}{R^2}\\
dB = \frac{\mu_0}{4\pi} \, \frac{I \, R d\theta \, \hat{\theta} ⨯ \hat{r}}{R^2}\\
∴ dB = \frac{\mu_0}{4\pi} \, \frac{I \, R d\theta}{R^2} \, (\hat{\theta} ⨯ \hat{r})\\
\)
Hence, total \(B\) at the center of a circular loop,
\(\large{B = \int_0^{2\pi} dB = (\hat{\theta} ⨯ \hat{r}) \, \frac{\mu_0}{4\pi} \, \int_0^{2\pi} \frac{I\,d\theta}{R}}\)
∴ \(B= \frac{\mu_0 \, I}{2R} \hat{k}\) where, \(\hat{\theta} ⨯ \hat{r} = \hat{k}\) is a unit vector align z-axis.
FAQs
Biot Savart law is a law of magnetism and magnetostatics, that establishes a relation between the magnetic field and the magnitude, direction, length, and proximity of the current-carrying conductor.
The difference between Biot Savart Law and Ampere law is that the latter takes symmetry into account since it’s a closed line integral(Amperian loop).
No, we cannot compute electric field intensity using Biot Savart law.