Wheatstone Bridge

A Wheatstone Bridge is an electrical circuit used to measure an unknown resistance by balancing two legs(one leg containing the unknown component) of the circuit.

History

The Wheatstone bridge was invented by British scientist, physicist and mathematician Samuel Hunter Christie in 1833 and later, improved by English scientist, Sir Charles Wheatstone in 1843.

Wheatstone Bridge Explained

So, let’s dive deep into the explanation of this concept.

Theory

The Wheatstone bridge works on the principle of null deflection, i.e. the ratio of their resistances are equal, and no current flows through the galvanometer. The bridge is very reliable and gives an accurate result.

The Wheatstone Bridge circuit is nothing more than two simple series-parallel arrangements of resistances connected between a voltage supply terminal and ground producing zero voltage difference between the two parallel branches when balanced. 

The circuit has two input terminals(current flowing in, at A, through R₁ and R₃) and two output terminals(current flowing out, at C, through R₂ and R_x) consisting of four resistors configured in a diamond-like arrangement as shown.

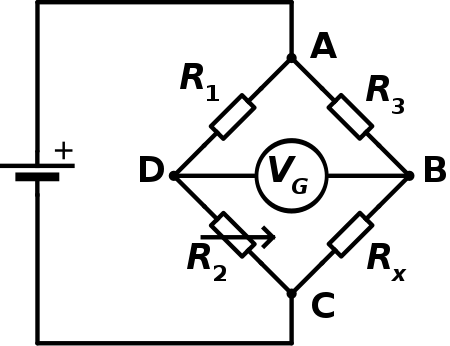
R_x – unknown resistance
R₁, R₂, R₃ – known resistances
V_G – Voltage source

In the above figure, R_x, R₁, R₃ are fixed resistances, while R₂ is adjustable resistance. So, R₂ is adjusted until the bridge is balanced, i.e., no current flows through the galvanometer.

At this point, the voltage between B and D will be zero.

This gives,
\(\frac{R_2}{R_1} = \frac{R_x}{R_3}\)

\(⇒ R_x = \frac{R_2}{R_1}.R_3\)

If R₁, R₂, and R₃ are known to a high precision, then R_x can be calculated to a high precision.

Derivation

Initially, Kirchoff’s First Law is used at B and D,
\(I_3 – I_x + I_G = 0\)
\(I_1 – I_2 – I_G = 0\)

Using Kirchoff’s second law in loops ABDA and BCDB,
\((I_3 . R_3) – (I_G . R_G) – (I_1 . R_1) = 0\)
\((I_x . R_x) – (I_2 . R_2) + (I_G . R_G) = 0\)

Since the bridge is balanced, 

Applications of Wheatstone Bridge

• The wheatstone bridges are used for the precise measurement of low resistance. The Kelvin bridge, Carey Foster bridge, etc., was specially adapted from the Wheatstone bridge for measuring very low resistances.
• Variations on the Wheatstone bridge can be used to measure capacitance, inductance, impedance and other quantities, such as the amount of combustible gases in a sample, with an explosimeter.
• Wheatstone bridges along with an operational amplifiers are used to measure the physical parameters like temperature, strain, light, etc. 

Limitations of Wheatstone Bridge

• These wheatstone bridges gives inaccurate readings if it is unbalanced.
• It is a very sensitive device.
• It is used for measuring resistances ranging from a few ohms to a few kilo-ohms.

Example

Question. In a Wheatstone’s bridge R₁ = 100 Ω, R₂ = 1000 Ω and R₃ = 40 Ω. If the galvanometer shows zero deflection, determine the value of the unknown resistor.

Solution. Given, R₁ = 100Ω, R₂ = 1000Ω and R₃ = 40Ω 

As we know,

\(R_x = \frac{R_2.R_3}{R_1}\)
\(⇒ R_x = \frac{1000 * 40}{100}\)
\(∴ R_x = 400 Ω\)

FAQs