De Morgan’s Law

De Morgan’s Law is one of the crucial laws in sets. Various operations are performed on sets like complement, union and intersection.

These operations and their usage are further simplified using laws known as De Morgan’s Laws.  

History

Augustus De Morgan was born in 1806 in Madurai, India. De Morgan’s work entitled Double Algebra and trigonometry consisting two parts.

The first stage in algebra is arithmetic, where only natural numbers and symbols of operations such as +, \(\times \), etc. are used. 

The next stage is universal arithmetic, where variables are used instead of numbers, to denote numbers universally, and the processes are conducted.

De Morgan’s First Law

In De Morgans’s first law, the complement of the union of two sets A and B is equal to the intersection of the complement of the sets A and B.

(A \(\cup\) B)’= A’ \(\cap\) B’ 

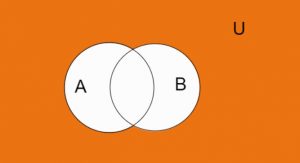
The white colour shows the union of the two sets A and B. The Orange color shows the complement of the union, which is all the area except the area contained in the union.

(A \(\cup\) B) = area either in A or B

Hence, 

(A \(\cup\) B)’ = area commonly excluding for A or B

I.e., area contained in A’ and B’ 

That is the area A’ \(\cap\) B’

De Morgan’s Second Law

According to De Morgan’s second law, the complement of the Intersection of two sets A and B is equal to the Union of the complement of the sets A and B.

(A \(\cap\) B)’= A’ \(\cup\) B’ 

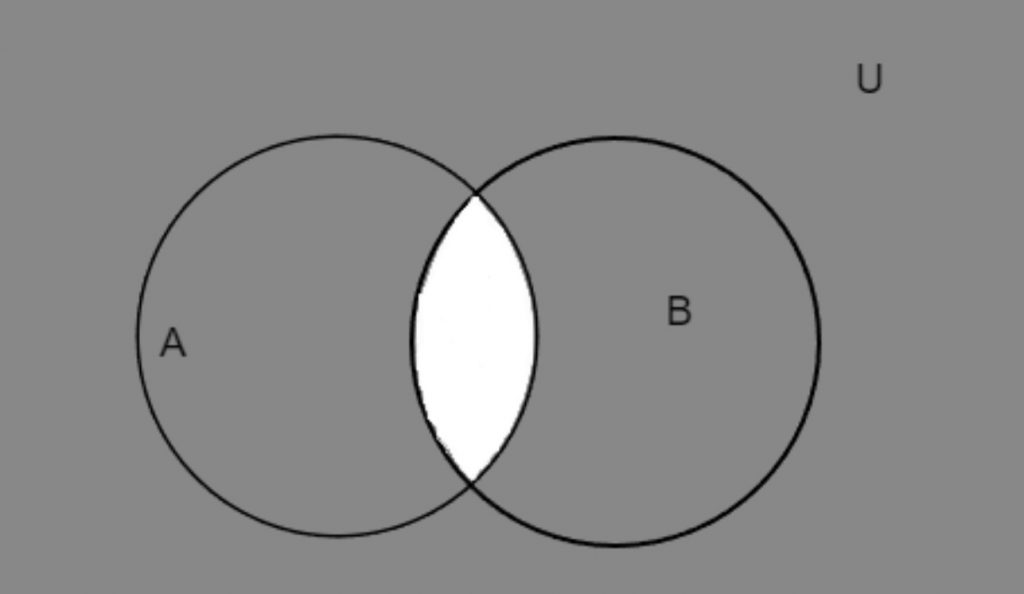
The white color shows the intersection of the two sets A and B. The gray color shows the complement of the intersection, which is all the area except the area contained in the intersection.

(A \(\cap\) B) = area both in A or B

Hence, 

(A \(\cap\) B)’ = area in U except the A \(\cap\) B

I.e., the area  outside (A \(\cap\) B) 

That is the area A’ \(\cup\) B’

Examples

1. If U = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}; A = {1, 4, 7, 10}; B = {2, 4, 6, 8, 10}. Prove Demorgan’s First Law.

Sol: De Morgans First Law gives us (A \(\cup\) B)’= A’ \(\cap\) B’ 

Taking RHS A’ = {2, 3, 5, 6, 8, 9} & B’ = {1, 3, 5, 7, 9}

A’ \(\cap\) B’ = {3, 5, 9}

Whereas LHS, A \(\cup\) B = {1, 2, 4, 6, 7, 8, 10}

(A \(\cup\) B)’ = {3, 5, 9} = RHS (Thus proving the law)

2. If U = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}; A = {1, 3, 5, 7, 9}; B = {2, 3, 7, 1}. Prove De Morgan’s Second Law.

Sol. De Morgan’s second Law gives us (A \(\cap\) B)’= A’ \(\cup\) B’ 

Taking RHS = A’ = {2, 4, 6, 8, 10} & B’ = {4, 5, 6, 8, 9}

A’ \(\cup\) B’ = {2, 4, 5, 6, 8, 9, 10}

Taking LHS = A \(\cap\) B = {1, 3, 7}

(A \(\cap\) B)’ = {2, 4, 5, 6, 8, 9, 10} = RHS (Thus proving the law)

FAQs

Related Topics