Set Operations

Set Theory and its Operations are probably the most fundamental branch of mathematics required for any thorough study of mathematics.

Mathematicians like George Cantor, Richard Dedekind, Zermelo, and Frankel developed our modern knowledge of set theory.

Set Theory comprises mathematical objects called Sets, and their operations are called set operations. This study expands our knowledge to learn about different types of set operations and their importance.

History 

A paper initiated set theory: “On a Property of the Collection of All Real Algebraic Numbers”(1874) by George Cantor. 

Around 1900 several paradoxes were found in the set theory by George cantor. 

The most well-known paradox was ‘Russell’s paradox’. These paradoxes gave rise to a need for a better set theory. Ernst Zermelo and Abraham Fraenkel developed the Zermelo-Fraenkel Set Theory today as a modern theory free of paradoxes.

Set Operations Explained

A set operation is a mathematical process that takes set(s) as input and gives an output (a number or a set).

Examples of set operations are – Union, Intersection, Difference, Complement, Cardinality, Cartesian product, Power set, etc.

Union of a Set

Let A and B be two sets. The union of A and B, denoted by \(A \cup B\), is the set that contains those elements that are either in A or in B, or both. No element is repeated .

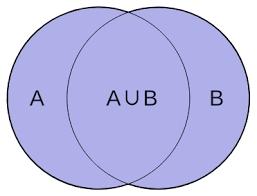
\(A \cup B = \{ x : x \in A \mbox{ or } x \in B  \}\)

Example: If \(A = \{ 1,2,3,4 \}\) and \(B = \{ 2, 5, 4, 6, 7 \}\), then \(A \cup B = \{ 1, 2, 3, 4, 5, 6, 7 \}\) .            

Some essential relations are:

1. If A is a non-empty set and B is a null set, then \(A \cup B = A\). 
2. If S is the universal set and A is a non-empty set, then \(A \cup S = S\).
3. \(A \cup B = B \cup A\) (Commutative)
4. \((A \cup B ) \cup C = A \cup ( B \cup C)\) (Associative)

Intersection of a Set

Let A and B be two sets. The intersection of A and B, denoted by \(A \cap B\), is the set that contains those elements that are in both A and B. No element is repeated .

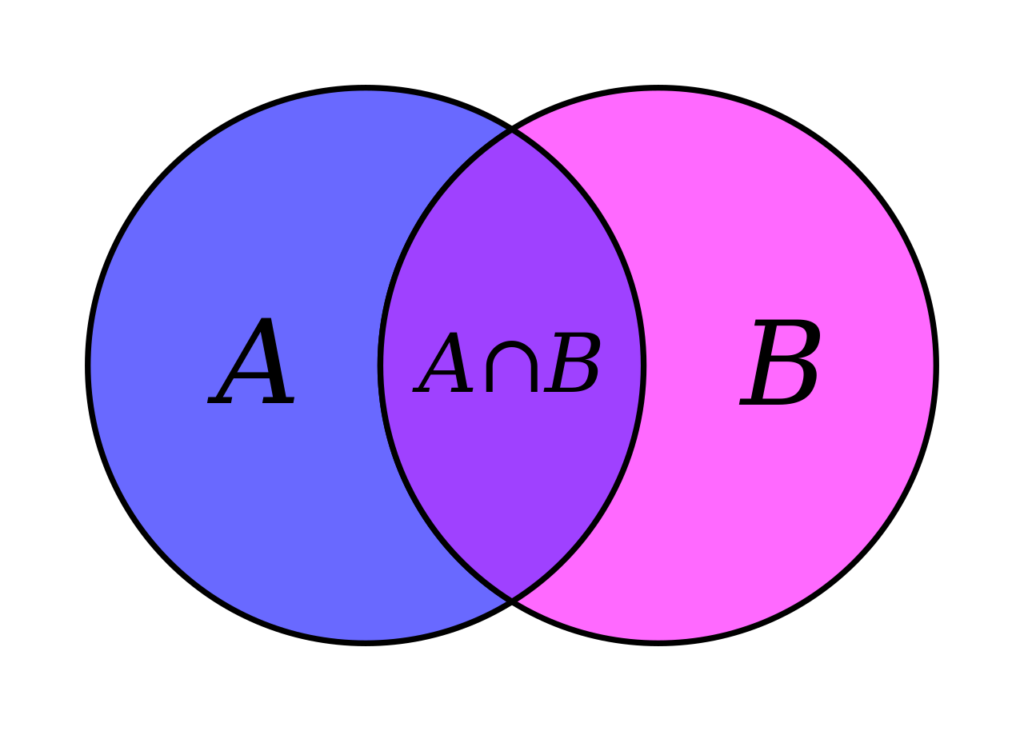
\(A \cap B = \{ x : x \in A \mbox{ and } x \in B \}\)

Example: If \(A =\{1, 2, 3, 4 \}\) and \(B = \{ 2, 5, 4, 6, 7 \}\), then \(A \cap B =\{ 2, 4 \}\).

Some essential relations are:                

1. If A is a non-empty set and B is a null set, then \(A \cap B = \phi\).
2. If S is the universal set and A is a non-empty set, then \(A \cap S = A\).
3. \(A \cap B = B \cap A\) (Commutative)
4. \((A \cap B) \cap C = A \cap (B \cap C)\) (Associative)

Difference of a Set

Let A and B be two sets. The difference of  A and B denoted by \(A – B\) is the set of all the elements of A which are not in B .

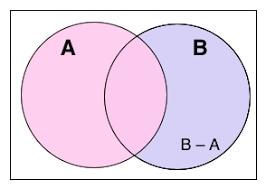
\(A – B = \{ x : x \in A \mbox{ and } x \not \in B \}\)

Example: If \(A = \{1, 2, 3, 4 \}\) and \(B = \{ 2, 5, 4, 6, 7 \}\), then \(A – B = \{ 1\}\) . Similarly, \(B – A = \{ 5, 6, 7 \}\).

Read About Types of Relations

Complement of a Set

Let A be any set and S be the Universal set. Then, A is a subset of S (\(A \subset S\)).

The complement of A, denoted by A’ or \(\bar{A}\) is \(A’ = S – A = \bar{A}\).

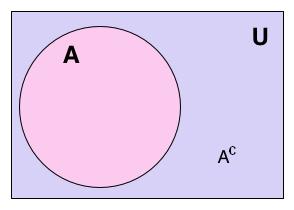
Example: If \(S = \{ 1, 2, \ldots , 10 \}\) and \(A = \{ 1, 2 , 3 \}\) then \(A’ = \{ 4, 5, \ldots , 10 \}\)

Some essential relations are:

1. If A is a null set, then \(A’ = S\)             .  
2. If S is a universal set, then \(S’ = \phi\).
3. \((A’)’ = A\).

Cardinality of a Set

The cardinality of a set is nothing but the number of elements of the set (non-repeating).

Example: If \(A = \{ 0, 1, 2, \ldots , 10 \}\)  then cardinality of A , denoted by \(n(A)\) is \(n(A) = 11\).

Cartesian Product of Sets

Let A and B be any two sets. The cartesian product or the cross product of A and B is a set \(A \times B\) containing all the ordered pair of A and B elements.

\(A \times B = \{ (x, y) :  \forall x \in A , y \in B  \}\)

Example: If \(A = \{ 1, 2, 3 \}\) and \(B = \{ 3, 4 \}\)  then,

\(A \times B = \{ (1, 3) , (1, 4), (2, 3), (2, 4), (3, 3) , (3, 4)  \}\)

Here, \(n(A) = 3\) , \(n(B) = 2\) and \(n(A \times B ) = 3 \times 2 = 6\).

The Power Set

The Power Set of a set is the set of all possible subsets of that set. If the given set’s cardinality is n, then the cardinality of the power set is \(2^n\).

Example: If \(A = \{ 1, 2 \}\), then power set of A , denoted as \(P(A)\), is

\(P(A) = \{ \phi , \{ 1 \} , \{ 2 \} , \{ 1, 2 \}  \}\)

Here , \(n(P(A)) = 2^2 = 4\).

Some Important Relations with Set Operations

1. \(n(A \cup B ) = n(A) + n(B) – n(A \cap B)\)
2. \(n(A \cup B \cup C  ) = n(A) +n (B) + n(C) – n(A \cap B) – n (A \cap  C) + n( A \cap B \cap C )\)
3. \(A \cup ( B \cap C ) = ( A \cup B ) \cap ( A \cup C )\) (Distributive)
4. \(A \cap ( B \cup C ) = ( A \cap B ) \cup ( A \cap C )\) (Distributive)
5. \(A \cup \phi = A\)
6. \(A \cup A’ = S\)
7. \(A \cap \phi = \phi\)
8. \(A \cap A ‘ = \phi\)
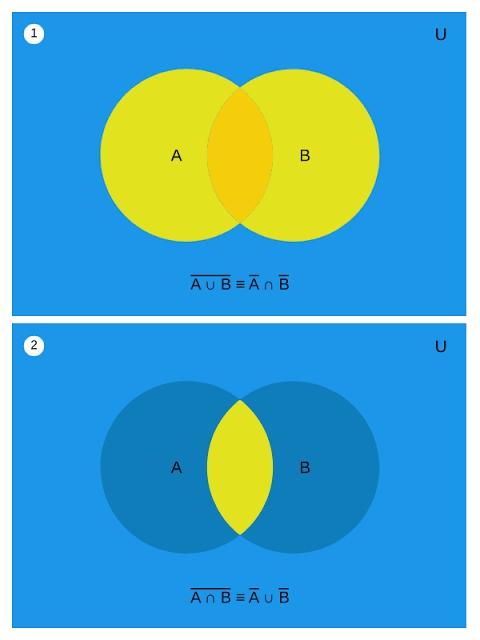
9. \((A \cup B)’ = A’ \cap B’\) (De Morgan’s Law)
10. \((A \cap B )’ = A’ \cup B’\) (De Morgan’s Law)

Applications of Set Theory and Operations

Set theory and set algebra find applications in a broad spectrum of fields- Statistics, Physics, Number Theory, Group Theory, Probability, Engineering, Economics, etc. Set Theory is mainly used a lot in the Study of Axiomatic Probability.

Most common sets:

\(\mathbb(R)\)  – Set of Real Numbers.
\(\mathbb(Z)\) – Set of Integers.
\(\mathbb(C)\) – Set of Complex Numbers.
\(\mathbb(N)\) – Set of Natural Numbers.
\(\mathbb(Q)\) – Set of Rational Numbers.
\(\mathbb(W)\) – Set of Whole Numbers.

Examples on Set Operations

Question 1.  Draw Venn diagrams for De Morgan’s Laws.

Answer.  De Morgans’s Law Venn diagram (Source)

Question 2. In a survey of 400 students in a school, 100 were listed as taking apple juice, 150 as taking the orange juice, and 75 were listed as taking both apples as well as orange juice. Find how many students were taking neither apple juice nor orange juice.

Answer. Let \(U\) denote the set of surveyed students, and \(A\) denote the set of students taking apple juice, and \(B\) denote the set of students taking orange juice. Then,

 \(n (U) = 400, n (A) = 100, n (B) = 150\) and \(n (A \cap B) = 75\).

Now, \(n (A′ \cap B′) = n (A \cup B)′\)

\(= n(U) – n(A \cup B)\)
\(= n (U) – n (A) – n (B) + n (A \cap B) \)
=>\(= 400 – 100 – 150 + 75 = 225\).

Hence 225 students were taking neither apple juice nor orange juice.

Question 3. List all the subsets of the set { –1, 0, 1 }.

Answer. Subsets are \(\phi , \{ -1\} , \{ 0 \} , \{ 1 \} , \{ -1, 0 \} , \{ -1, 1\} , \{ 0, 1\} , \{ -1, 0 , -1 \} \).

FAQs