Hyperbola vs Parabola is an interesting difference to study in geometry. Let us first see a few lines about these two curves and then go deep into hyperbola vs parabola.
Hyperbola is like an open curve with two branches. It is an intersection of a plane with both halves of a double cone. The plane doesn’t need to be parallel to the cone’s axis; the hyperbola will be symmetrical in any case.
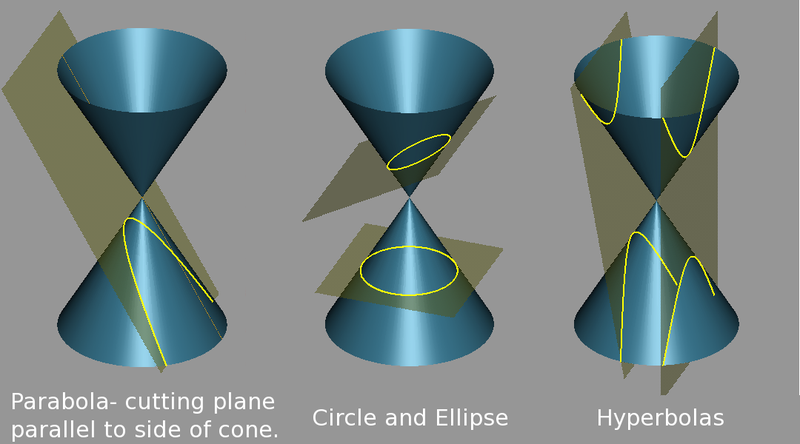
A parabola is a curve, where any point is at an equal distance from a fixed point (the focus), and a fixed straight line (the directrix).
Now let us see the history of both the curves.
Index
History
Menaechmus discovered Hyperbolae during his investigations of the problem of doubling the cube but later called sections of obtuse cones. The term hyperbola is believed to be coined by Apollonius of Perga in his definitive work, the Conics, on the conic sections.
Archimedes computed the area enclosed by a parabola and a line segment by the method of exhaustion, 3rd century BC.

The name “parabola” by Apollonius, who discovered many properties of conic sections. It means “application,” referring to “application of areas”.
What is a Parabola?
Parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped.
A plane curve generated by moving points so that its distance from a fixed point is equal to its distance from a fixed-line: the intersection of a right circular cone with a parallel plane to an element of the cone.
General Equation of Parabola
General equation of parabola is given by,
\(y^2 = \pm 4ax\) (directrix is parallel to y-axis), &
\(x^2 = \pm 4by\) (directrix is parallel to x-axis)
What is a Hyperbola?
The pair of hyperbolas are formed by the intersection of a plane and two equal right circular cones on opposite sides of the same vertex.
A hyperbola is the locus of all those points in a plane, such that the difference in the distances from two fixed points in the plane is a constant.
General Equation of Hyperbola
Taken as known the focus (h, k),
The formula for the Hyperbola can be given by,
\(\frac{(x-h)^2}{a^2} – \frac{(y-k)^2}{b^2} = 1\),
Here, \(a\) is the transverse axis & \(b\) is the conjugate axis.
Let, the directrix of parabola be \(y = mx + b\), then the equation is given as
\(\frac{[y – mx – b]^2}{[m^2 + 1]} = (x – h)^2 + (y – k)^2\)
Eccentricity
The eccentricity is the distance ratio from the centre to a vertex and from the centre to a focus(foci). It is denoted by \(e\).
Eccentricity of Hyperbola = \(\frac{c}{a}\)
Eccentricity of hyperbola is always \(\geq 1\).
Since, \(c \geq a\)
The eccentricity of Parabola is 1.
Latus Rectum
The line segments perpendicular to the transverse axis through any of the foci such that their endpoints lie on the curve are defined as the latus rectum.
The Latus Rectum in Hyperbola is given by \(\frac{2b^2}{a}\).
The Latus Rectum of Parabola is given by \(4a\).
Applications
The main application of parabolas is their reflective properties (lines parallel to the axis of symmetry reflect the focus).
Hyperbola is handy in real-world applications like telescopes, headlights, flashlights, lampshades, Gear transmission, structure for Coal-fired Power Plants, etc.
These are frequently used in physics, engineering, and many other areas.
Examples
Question 1. Find the points of intersection of the two parabolas with equation \(y = -(x – 3)^2 + 2\) and \(y = x^2 – 4x + 1\).
Solution. Given,
\(y = -(x – 3)^2 + 2 … (1)\)
and, \(y = x^2 – 4x + 1 … (2)\)
Equating (1) & (2) we get,
\(-(x – 3)^2 + 2 = x^2 – 4x + 1\)
\(\Rightarrow – 2x^2 + 10x – 8 = 0\)
\(\Rightarrow -x^2 + 5 x – 4 = 0\)
Therefore \(x = 1, 4\)
Using equation to find y, we get,
\(x = 1\) in (1) \(\Rightarrow y = -(x – 3)^2 + 2\)
\(\Rightarrow y= -(1 – 3)^2 + 2 = – 2\)
\(x = 4\) in (2) \(\Rightarrow y = -(x – 3)^2 + 2\)
\(\Rightarrow y = -(4 – 3)^2 + 2 = 1\)
Therefore, the points of intersection are \((1 , -2)\) and \((4 , 1)\).
Question 2. Calculate the equation of the hyperbola with a transverse axis of 8 and a focal length of 10.
Solution. Given,
Transverse axis \((2a) = 8\) & Focal length \((2c) = 10\).
Therefore \(a = 4\) & \(c = 5\)
As we know, by the formula
\(b^2 = c^2 – a^2\)
Therefore, \(b = \sqrt{25 – 16} = 3\)
Hence, the equation of hyperbola is
\(\frac{x^2}{4^2} – \frac{y^2}{3^2} = 1\)
FAQs
The parabola is a single open curve with eccentricity one, whereas a hyperbola has two curves with an eccentricity greater than or equal to one. Both have an open curve that extends to infinity.
Hyperbolas, as well as non circular ellipses, have two associated directrices and two distinct foci.
Each directrix being perpendicular to the line joining the two foci.
The eccentricity shows us how “un-circular” a given curve is
Circle has eccentricity = 0,
Parabola has eccentricity = 1
Hyperbola has eccentricity \(\geq\) 1
For infinite eccentricity, we get a line.
So, that was all about hyperbola vs parabola and I hope that you got to learn about both the curves and their differences
