A magnetic field is produced whenever an electrical charge is in motion. An electron orbiting the nucleus of an atom produces the magnetic field as does an electrical current flowing through a wire. The direction and charge of the particle determine the direction of the magnetic field.
Magnetic fields exert forces on moving charges. The direction of force is perpendicular to the direction of the motion of the charge. In this article, we will see some important formulas for magnetism and current which will also help you in preparation for competitive exams like JEE and NEET.
1. Magnetic field due to a moving point charge
\(\overrightarrow{dB} = \frac{\mu_{o}}{4\pi}\cdot \frac{q(\overrightarrow{v}\times\overrightarrow{r})}{r^{3}}\)
2. Biot-savart’s Law
\(\overrightarrow{dB} = \frac{\mu_{o}I}{4\pi}\cdot \left(\frac{\overrightarrow{dl}\times\overrightarrow {r}}{r^{3}}\right)\)
3. Magnetic field due to a straight wire
\(B = \frac{\mu_{o}}{4\pi}\frac{I}{r}(sin\theta_{1}+sin\theta_{2})\)
4. Magnetic field due to infinite straight wire
\(B = \frac{\mu_{o}}{2\pi}\frac{I}{r}\)
5. Magnetic field due to circular loop
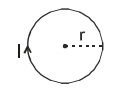
(i) At centre \(B = \frac{\mu_{o}NI}{2r}\)
(ii) At axis \(B = \frac{\mu_{o}}{2}\left ( \frac{NIR^{2}}{(R^{2}+x^{2})^{3/2}} \right )\)
6. Magnetic field on the axis of the solenoid
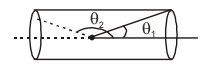
\(B = \frac{\mu_{o}nI}{2}(cos\theta_{1}-cos\theta{2})\)
7. Ampere’s Law
\(\oint \overrightarrow{B}\cdot\overrightarrow{dl} = \mu_{o}I\)
8. Magnetic field due to long cylindrical shell
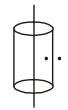
B = 0, r < R
\(= \frac{\mu_{o}}{2\pi}\frac{I}{r}, r \geq R \)
9. Magnetic force acting on a moving point charge
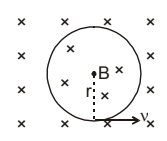
a) \(\overrightarrow{F} = q(\overrightarrow{v}\times\overrightarrow{B})\)
(i) \(\overrightarrow{v} \perp \overrightarrow{B}\)
\(r = \frac{mv}{qB}\)
\(T = \frac{2\pi m}{qB}\)
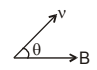
(ii) \(r = \frac{mvsin\theta}{qB}\)
\(T = \frac{2\pi m}{qB};\) \(Pitch = \frac{2\pi mvcos\theta}{qB}\)
b) \(\overrightarrow{F} = q\left [ (\overrightarrow{v}\times\overrightarrow{B}) + \overrightarrow{E} \right ]\)
10. Magnetic force acting on a current carrying wire
\(\overrightarrow{F} = I\left ( \overrightarrow{l}\times \overrightarrow{B} \right )\)
11. Magnetic Moment of a current carrying loop
\(M = N \cdot I \cdot A\)
12. Torque acting on a loop
\(\overrightarrow{\tau} = \overrightarrow{M}\times \overrightarrow{B}\)
13. Magnetic field due to a single pole
\(B = \frac{\mu_{o}}{4\pi}\cdot\frac{m}{r^{2}}\)
14. Magnetic field on the axis of magnet
\(B = \frac{\mu_{o}}{4\pi}\cdot\frac{2M}{r^{3}}\)
15. Magnetic field on the equatorial axis of the magnet
\(B = \frac{\mu_{o}}{4\pi}\cdot\frac{M}{r^{3}}\)
16. Magnetic field at point P due to magnet