Factors Of 35

Factors of 35 are the set of integers that can divide it perfectly i.e when you divide 35 with its factors, we will get 0 as the remainder.

Let us see the list of factors 35, different ways to represent the factors and various methods to find these factors.

1. Factors: 1, 5, 7 and 35
2. Negative Factors: -1, -5, -7 and -35
3. Prime Factors: 5, 7
4. Prime Factorization : 5 × 7 = 5 × 7
5. Sum of Factors: 48

Now the most used method to find factors in the prime factorization

Prime Factorization

The prime factorization of 35 refers to the process of writing the number as the product of its prime factors.

There are two methods of prime factorization which we can follow to find all the factors of a number

Prime Factorization of 35 By Upside Down Division Method

The Prime Factorization by Upside Down Division Method is shown below:

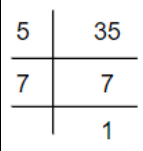
From this, we can get the factors as 1, 7, 5, 35

So, basically, after completing this procedure we will just have to list down all the left and right side numbers and we will get the list of all the factors of the number by that.

Prime Factorization of 35 By Factor Tree Method

 To use this method to find the factors of a number say x,

1. Firsly consider two factors say a,b of x such that a*b is equal to x. Check if both are primes, if yes, stop the process, If no go to step 2.
2. In a,b if anyone of it is composite, again break it down into two factors. If both the factors are prime stop it there orelse keep repeating the process.

You may have different factor trees depending on the starting point, however, all of them would show the same prime factors.

Factor Tree Method is shown below:

We stop the factor tree because 5 and 7 both are prime numbers and cannot branch further. As a result, the prime factorization of 35 is 5×7

FAQs

More factors: