Factors of 45 are basically the numbers that divide it evenly or exactly without leaving any remainder i.e if a number divides 45 with a remainder of zero, then that number is called a factor.
- All Factors: 1, 3, 5, 9, 15 and 45
- Factors in pairs: (1, 45), (3, 15), and (5, 9)
- Prime Factors of 45: 3, 5
Now, let us see the prime factors and prime factorization of the number.
Index
Prime Factorization Of 45
Prime factorization is a method of “expressing” or finding the given number as the product of prime numbers. If a number occurs more than once in prime factorization, it is usually expressed in exponential form to make it more compact.
Here, prime factorization comes out to be : 3 x 3 x 5
Prime Factorization Of 45 By Upside Down Division Method
Upside-Down Division is one of the techniques used in the Prime factorization method to find factors of numbers.
In this method, you will divide a given “composite” number evenly by the several prime numbers(starting from the smallest) till it gets a prime number.
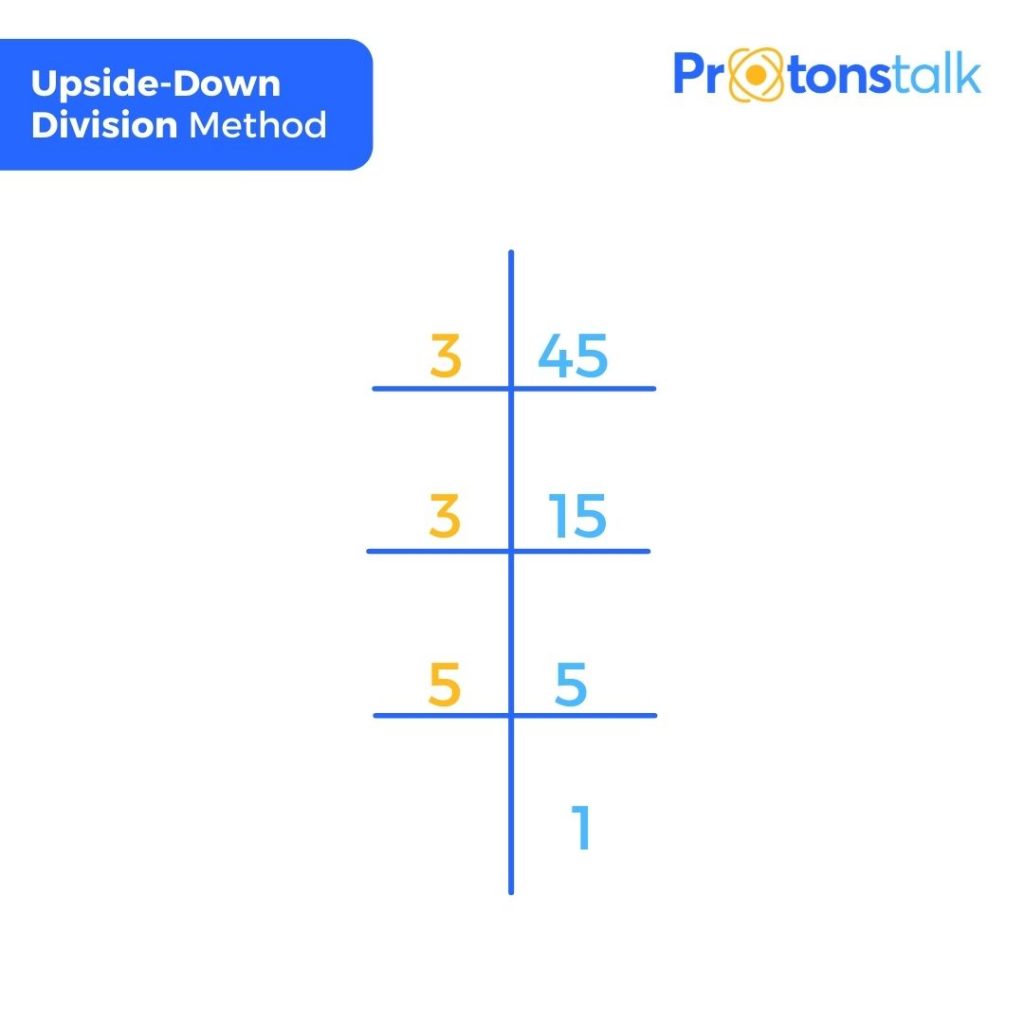
It is called Upside-Down Division because the symbol is flipped upside down.
Here, 45 is an odd number. So it is undoubtedly divisible by 3 with no remainder.
Thus we do 45÷ 3 = 15. Now find the prime factors of the obtained quotient.
Repeat Step 1 and Step 2 until we get a result of prime number as the quotient. Here, 15 is the quotient. Now find the prime factor of 15
15÷ 3 = 5. Here, 5 is the prime number.
So we can stop the process.
So, now the prime factorization of 45 with the upside-down division method is 3 × 3 × 5.
Prime Factorization Of 45 By Factor Tree Method
The Factor tree method is another technique for producing the prime factorization and all factors of a given number.
To use this method for a number x,
Firstly consider two factors say a,b of x such that a*b is equal to x and at least one of them (a, b) is a prime factor say a.
Then consider two factors of b say c, d such that again at least one of them is a prime factor. This process is repeated until both the factors are prime i.e if we get both the factors as prime at any step, we stop the process there.
Following is the factor tree of the given number.
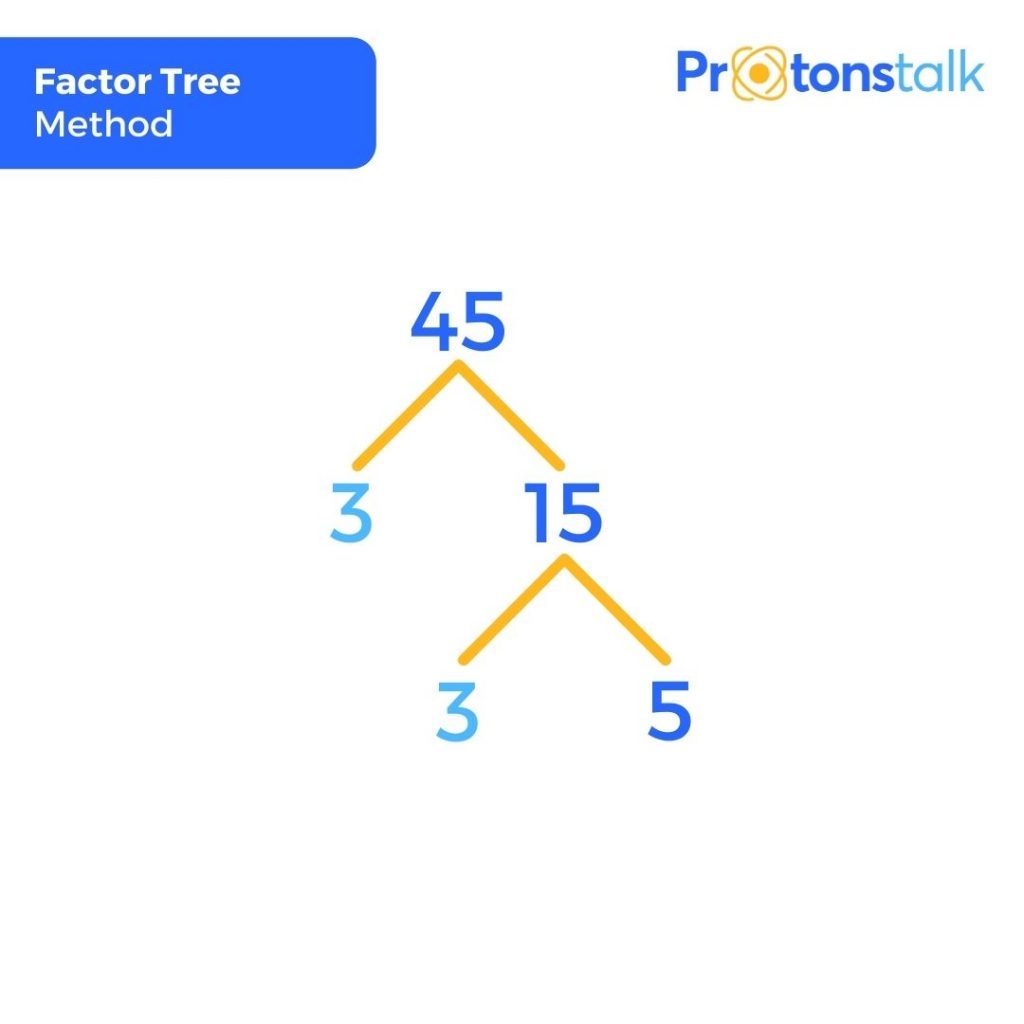
Here we can get the prime factorisation of 45 as 3 * 3 * 5 and the two prime factors are 3, 5
FAQs
The factors of given numbers are 1, 2, 4, 7, 14, 28 and 1, 3, 5, 9, 15, 45 respectively. So, there is only one common factor and it one and thus both of them can be called as coprimes.
Sum of all its factor is = (3(2+1)-1)/(3-1) * (5(1+1)-1)/(5-1) = 78. (Using the formula for finding the sum of factors of a number)
The factors of the given numbers respectively are 1, 3, 5, 9, 15, 45 and 1, 2, 4, 5, 8, 10, 20, 40, respectively.
We can see that [1, 5] are common factors.
Therefore, the Greatest Common Factor of 45 and 40 is 5.
More factors:
