Inverse Function Calculator is an online tool to calculate the inverse of any given function. An Inverse Function also called anti function is a function which “reverses” any real-valued function f(x) and is denoted by \(f^{-1}\).
About Inverse Function Calculator
Input
The inputs of the calculator are
- The function for which you want to find an inverse
Steps
Inverse function calculator is a user-friendly tool. The following is the detailed step-by-step process to find the inverse of any function.
- Enter any function in the respective input field against the text “Inverse function of“
- Click on submit button to formulate the inverse of that function.
- The output i.e the inverse function is displayed in a separate window.
Output
The outputs of the calculator is
- The entered function
- The inverse of the given function
Inverse of a Function
Let f be a function whose domain is the set X, and whose codomain is the set Y. Then f is invertible if and only if there exists a function \(f^{-1}\) with domain Y and codomain X, with the property \( f(x)=y \Leftrightarrow f^{-1}(y)=x.\)
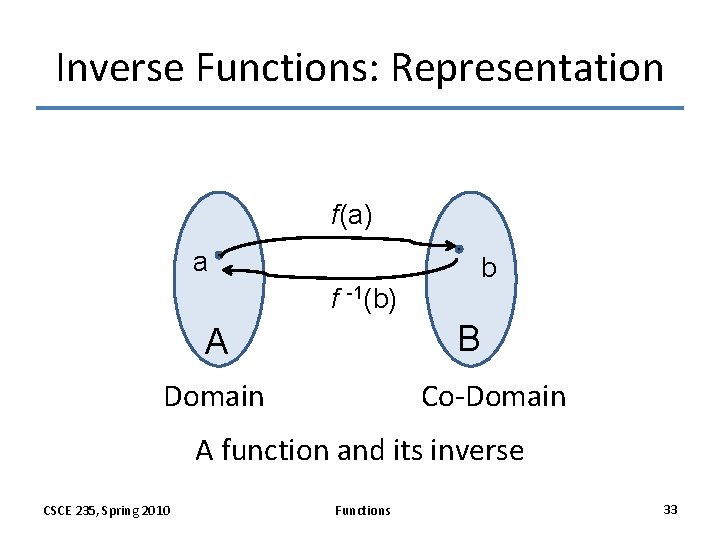
In other words, if f is any function with input x that gives an output y, then its inverse function, denoted by, \(f^{-1}\) is applied to y to give output as x.
However, not all functions are invertible. The inverse of a function exists only when every element \(y \in Y\) must correspond to no more than one element \(x \in X\).
For every injection i.e \(f:X \rightarrow Y\) , it is necessary for the surjection i.e \(f^{-1}:Y \rightarrow X\) to exist in order to compute the inverse of a function. Such functions whose both injection and surjection exists is called a Bijective function.
In another convention namely, the Set-theoretic or the Graph definition, the functions are defined using ordered pairs. In this convention, the codomain and the image of the function are made similar.
Self Inverse Function
For a function \(f:X \rightarrow X\), If X is a set, then its inverse function is the identity function on X \(id^{-1}_{x}=id_{x}\).
Example:
Find the inverse of \(f(x)=\sqrt{x-3}\)
Solution :
\( y=\sqrt{x-3}\\x=\sqrt{y-3}\)by squaring it on both sides
\( x^{2}=y-3\\x^{2} + 3=y\\f^{-1}(x) = x^{3}+3\)Checkout More Calculators Here
