The secant function ‘or’ Sec Theta is one of the trigonometric functions apart from sine, cosine, tangent, cosecant, and cotangent. In right-angled trigonometry, the secant function is defined as the ratio of the hypotenuse and adjacent side.
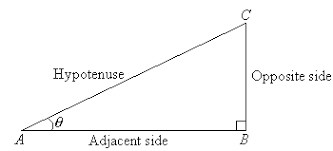
The mathematical denotation of the secant function is,
\(\sec(\theta) = \frac{\text{Hypotenuse Side}}{\text{Adjacent Side}}\)Index
More About Sec Theta
The derivative of \(\sec(\theta)\) in calculus is \(\sec(\theta) \tan(\theta)\) and the integral of it is \(\ln|\sec(\theta) + \tan(\theta)|\). The reciprocal of \(\sec(\theta)\) is \(\cos(\theta)\).
Below is a table of sec theta values for different degrees and radians.
| Radians | Degree | Tangent Value |
| 0 | 0° | 1 |
| \(\frac{\pi}{6}\) | 30° | \(\frac{2}{\sqrt{3}}\) |
| \(\frac{\pi}{4}\) | 45° | \(\sqrt{2}\) |
| \(\frac{\pi}{3}\) | 60° | 2 |
| \(\frac{\pi}{2}\) | 90° | \(\infty\) |
| \(\pi\) | 180° | -1 |
| \(\frac{3\pi}{2}\) | 270° | \(\infty\) |
| \(2\pi\) | 360° | 1 |
Important Sec Theta Formula
Some important properties of the secant function and sec theta formula are:
- \(\sec(-x) = \sec(x)\)
- \(\sec(90° – x) = cosec(x)\)
- \(\sec(x + 2\pi) = \sec(x)\)
- \(\sec(\pi – x) = -\sec(x)\)
- \(\sec^2(x) = 1 + \tan^2(x)\)
- \(sec(x + y) = \frac{\sec(x) \sec(y)}{1 – \tan(x) \tan(y)}\)
Solved Examples
Question 1. If \(\cos(x) = \frac{3}{5}\), calculate the value of \(\sec(x)\).
Solution. Using trigonometric identity,
\(\sec(x) = \frac{1}{\cos(x)} = \frac{1}{3/5}\)
\(∴ \sec(x) = \frac{5}{3}\)
Question 2. If \(\tan(\frac{x}{2}) = \frac{5}{8}\), calculate the value of \(\sec(x)\).
Solution. Using trigonometric identity,
\(\begin{align}
\sec^2(x) & = 1 + \tan^2(x)\\
& = 1 + (\frac{5}{8})^2\\
& = \frac{89}{64}\\
\sec(x) & = \frac{\sqrt{89}}{8}\\
\end{align}
\)
Question 3. Prove \(\sec(x + y) = \frac{\sec(x) \sec(y)}{1 – \tan(x) \tan(y)}\)
Solution. As we know,
\(\sec(x) = \frac{1}{\cos(x)}\) and \(\tan(x) = \frac{\sin(x)}{\cos(x)}\)
Considering RHS of given equation,
\(\begin{align}
\frac{\sec(x) \sec(y)}{1 – \tan(x) \tan(y)} & = \frac{\frac{1}{\cos(x)} \times \frac{1}{\cos(y)}}{1 -\frac{\sin(x)}{\cos(x)} \times \frac{\sin(x)}{\cos(y)}}\\
& = \frac{1}{\cos(x) \cos(y) – \sin(x) \sin(y)}\\
& = \frac{1}{\cos(x + y)}\\
& = \sec(x + y)\\
\end{align}
\)
Hence, LHS = RHS … Proved
FAQs
As we know, the angle (-x) lies in the 4th quadrant of a graph, and the secant is positive in this quadrant. Hence, sec(-x) = sec(x).
Sec theta of an angle in a right-angled triangle is defined as the ratio of the hypotenuse and adjacent side.
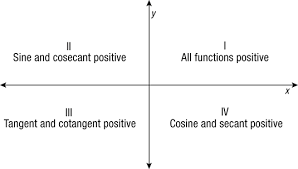
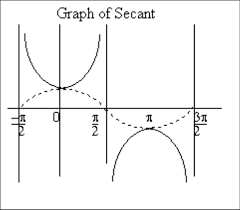
It can be observed from the above graph that sec(x) is positive in the 1st and 4th quadrants and negative in the 2nd and 3rd quadrants.
Know More Trigonometric Function
