Rectilinear Motion (or Linear Motion) is a specific form of motion. It is a motion that occurs in a single direction or axis. All the motion-related parameters are along one direction. Hence, the motion is also called motion in one dimension.
Index
Rectilinear Motion Definition
Rectilinear motion definition can be stated as a motion that occurs along a single direction only. It can also be called straight-line motion. The entire motion can be described without needing to use vectors.
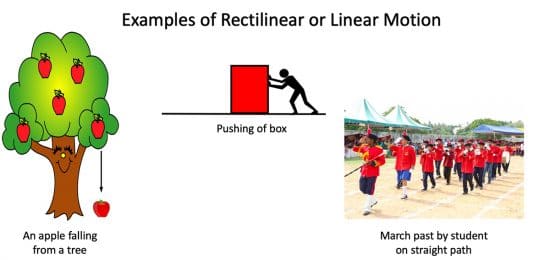
Rectilinear Motion Examples
Here are some of the rectilinear motion examples from our daily life.
- An athlete running on a track
- A bead moving on a fixed rod
- A train moving on a straight track
- Swimmer swimming in parallel
- An object falling straight down
Quantities Involved
Here we discuss some quantities involved in linear motion.
Distance
It is the total distance covered by the moving object/particle. For example, if an object moves 10 meters forward and 6 meters backwards, the total distance covered is 10+6 = 16 meters.
Displacement
It is the NET distance between starting and endpoint of motion. Using the same example as above, if the body moves 10 m forwards and 6 m backwards, it is only (10-6) m away from starting point. Thus, displacement is just 4 meters.
Velocity
Velocity \((\mathbf{v})\) is the rate of change of displacement. It has a direction. In linear motion, this direction is represented by a positive or negative sign. The boldface indicates the fact that it has a direction.
Average Velocity
It is given by the displacement \(\mathbf{s_2 – s_1}\) divided by the total interval of time \((t_2 – t_1)\) it takes cover.
In other words,
\(\bar{\mathbf{v}} = \frac{\mathbf{s_2-s_1}}{t_2 – t_1}\)
Instantaneous Velocity
It is the limit of average velocity when time interval goes to zero. It gives the velocity of an object at a specific instant.
\(\mathbf{v} = \lim_{{(t_2 – t_1)} \rightarrow 0} \frac{\mathbf{s_2-s_1}}{t_2-t_1} = \lim_{{\Delta t} \rightarrow 0} \frac{\mathbf{\Delta s}}{\Delta t} = \frac{d\mathbf{s}}{dt}\)
Thus, it is the time-derivative of displacement.
Speed
Speed (\(v)\) is the magnitude of velocity. As such, it has no direction and is always non-negative. Unlike velocity, it is denoted without boldface as it has no direction.
Average Speed
It is denoted by \(\bar{v}\). It can be given by distance (\(Delta d)\) covered in a given time interval \((\Delta t)\).
Mathematically,
\(\bar{v} = \frac{\Delta d}{\Delta t}\)
Acceleration
It is the rate of change of velocity. It is denoted by \(\mathbf{a}\). The boldface denotes that it has direction. In linear motion, the direction is given by the sign.
Mathematically,
\(\mathbf{a} = \frac{d\mathbf{v}}{dt} = \frac{d^2 \mathbf{s}}{dt^2}\)
Types of Rectilinear Motion
Now, let us discuss different types of rectilinear motion we encounter on daily basis.
Uniform Rectilinear Motion
In this type of linear motion, velocity is constant. There is no acceleration and no net external force acting on the object.
Uniformly Accelerated Rectilinear Motion
In this linear motion, velocity is changing but the acceleration is constant also known as Kinematic Equations. The motion of the body an be given by the three equations of motion
\(\mathbf{v} = \mathbf{u} + \mathbf{a}t\)
\(\mathbf{s} = \mathbf{u}t + \frac{1}{2} \mathbf{a} t^2\)
\(\mathbf{v^2} – \mathbf{u^2} = 2 \mathbf{a} \cdot \mathbf{s}\)
Know more on Rectilinear Motion Formula
Non-uniformly Accelerated Rectilinear Motion
Here, neither velocity nor acceleration is constant. Both can vary with time.
FAQs
It is a type of motion that happens along one direction or axis only. It is also known as linear motion.
Velocity is the rate of change of displacement, it has both magnitude and direction, while speed is simply the magnitude of velocity, it doesn’t have direction.
The three equations of motion are:
\(\mathbf{v} = \mathbf{u} + \mathbf{a}t\)
\(\mathbf{s} = \mathbf{u}t + \frac{1}{2} \mathbf{a} t^2\)
\(v^2 – u^2 = 2 \mathbf{a} \cdot \mathbf{s}\)
They are applicable for uniformly accelerated motion.
Rectilinear motion occurs in a single direction, and is thus one-dimensional. It can be called motion in a straight line.
Curvilinear motion occurs along a curve rather than a line. It can thus be two- or three-dimensional.
