The cotangent function ‘or’ cot theta is one of the trigonometric functions apart from sine, cosine, tangent, secant, and cosecant. The cotangent function in right-angle triangle trigonometry is defined as the ratio of the adjacent side to the opposite side.
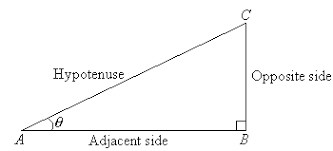
The mathematical denotation of the cotangent is,
\(\cot(\theta) = \frac{\text{Adjacent Side}}{\text{Opposite Side}}\)Index
More About Cot Theta
Cot theta can also be calculated from the ratio of the cosine of the angle to the sine of the angle.
\(\cot(\theta) = \frac{\cos(\theta)}{\sin(\theta)}\)
The derivative of \(\cot(\theta)\) in calculus is \(-cosec^2(\theta)\) and the integral of it is \(\ln|\sin(\theta)|\). The reciprocal of \(\cot(\theta)\) is \(\tan(\theta)\).
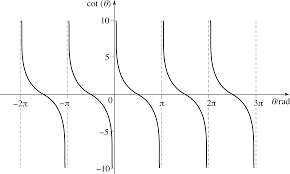
Below is a table of cotangent values for different degrees and radians.
| Radians | Degree | Cotangent Value |
| 0 | 0° | \(\infty\) |
| \(\frac{\pi}{6}\) | 30° | \(\frac{3}{\sqrt{3}}\) |
| \(\frac{\pi}{4}\) | 45° | 1 |
| \(\frac{\pi}{3}\) | 60° | \(\frac{1}{\sqrt{3}}\) |
| \(\frac{\pi}{2}\) | 90° | 0 |
| \(\pi\) | 180° | \(\infty\) |
| \(\frac{3\pi}{2}\) | 270° | 0 |
| \(2\pi\) | 360° | \(\infty\) |
Important Cot Theta Formula
Some important properties of the cotangent function and cot theta formula are:
- \(\cot(-x) = -\cot(x)\)
- \(\cot(90°-x) = \tan(x)\)
- \(\cot(x + \pi) = \cot(x)\)
- \(\cot(\pi – x) = -\cot(x)\)
- \(\cot^2(x) = cosec^2(x) – 1\)
- \(\cot(x + y) = \frac{\cot(x) + \cot(y)}{\cot(x) * \cot(y) – 1}\)
- \(\cot(x – y) = \frac{\cot(y) – \cot(x)}{\cot(x) * \cot(y) + 1}\)
Solved Examples
Question 1. If \(\sin(x) = \frac{4}{5}\), calculate the value of \(\cot(x)\).
Solution. Using trigonometric identity,
\(cos^2(x) = 1 – sin^2(x) = 1 – \frac{16}{25} = \frac{9}{25}\)
\(\cos(x) = \frac{3}{5}\)
Now,
\(\tan(x) = \frac{\sin(x)}{\cos(x)} = \frac{\frac{4}{5}}{\frac{3}{5}}\)
\(\tan(x) = \frac{4}{3}\)
As we know,
\(\cot(x) = \frac{1}{\tan(x)}\)
\(∴ \cot(x) = \frac{3}{4}\)
Question 2. If \(\sec(x) = \frac{5}{8}\), calculate the value of \(\tan(x)\).
Solution. Using trigonometric identity,
\(\tan^2(x) = sec^2(x) – 1 = (\frac{5}{8})^2 – 1 = \frac{25}{64} – 1 = -\frac{39}{64}\)
\(∴ \tan(x) = \sqrt{-\frac{39}{64}}\)
Question 3. John is standing on the ground and looking at the top of a tower with an angle of elevation of 60°. The distance between John and the tower is 15 feet. Calculate the height of the tower.
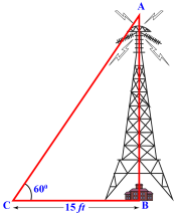
Solution. As we know,
\(\tan(\theta) = \frac{\text{Opposite}}{\text{Adjacent}}\)
\(\tan(60°) = \frac{\text{Opposite}}{\text{15}}\)
\(\sqrt{3} = \frac{\text{Opposite}}{\text{15}}\)
\(\text{Opposite} = 15 \sqrt{3}\)
∴ The height of the tower is \(15 \sqrt{3}\) feet.
FAQs
As we know, \(\cot(x) = \frac{\sin(x)}{\cos(x)}\). The angle (-x) lies in the 4th quadrant of a graph, and sine is negative in this quadrant and cos is positive. So, the ratio is negative. Hence, this shows that cot(-x) = -cot(x).
Cot theta of a right-angled triangle is equal to the ratio of the length of the opposite side to the length of the adjacent side. It is also equal to the ratio of the cosine of the angle and the sine of the angle.
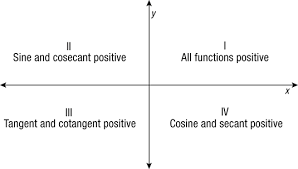
It can be observed from the above graph that cot(x) is positive in the 1st and 3rd quadrants and negative in the 2nd and 4th quadrants.
Know More Trigonometric Function
