The Golden Triangle, often known as the sublime triangle, is an isosceles triangle. The ratio of the side ‘a’ to base ‘b’ is equal to the golden ratio, \(\frac{a}{b} = \varphi\).
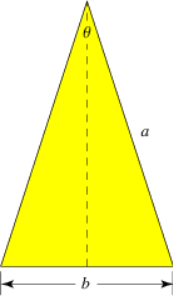
Considering the above figure, the vertex angle will be:.
\(\theta = 2sin^{-1}(\frac{b}{2a}) = 2sin^{-1}(\frac{1}{2\varphi}) = \frac{1}{5}\pi = 36^{\circ}\)
And then the height(h) to base(b) of the traingle will be related as,
\(4h^2 = b^2 (5+ 2 \sqrt{5})\)
Golden Ratio
Two quantities are in the golden ratio, if the ratio of the quantities is same as the ratio of their sum to the larger of the two quantities. Algebraically expressed, for quantities ‘a’ and ‘b’ with a > b > 0,
\(\frac {a+b}{a} = \frac {a}{b} = \varphi\)
Where, Greek letter phi(\(\varphi\) or \(\phi\)) represents the golden ratio. It is an irrational number that is a solution to the quadratic equation \(x^2 − x − 1 = 0\) , with a value of,
\(\varphi = \frac {1+{\sqrt {5}}}{2}=1.6180339887\ldots \).
Because of its frequent appearance in geometry, Ancient Greek mathematicians first studied what we now call the golden ratio.
Applications of Golden Triangle
Some points of a logarithmic spiral are formed using golden triangles.
This triangle is used in determining the dimensions of the layout in Architecture.
The golden triangle is classically used in paintings and photography to visual presentation for paintings and photographs, especially those that have elements with diagonal lines.
FAQs
Golden triangle is such that the ratio of the hypotenuse ‘a’ to base ‘b’ is equal to the golden ratio, \(\frac{a}{b} = \varphi\).
The Golden Triangle is an isosceles triangle with a vertex angle of 36° and base angles of 72°. When a base angle is bisected, the angle bisector divides the opposite side in a golden ratio and forms two smaller isosceles triangles.
Know about more interesting triangles herre
