Carnot Engine

A Carnot Engine or a Carnot Heat Engine is a heat engine that operates on the Carnot cycle.

Basic model for the Carnot engine was developed in 1827, by Nicolas Leonard Sadi Carnot. The model was later graphically expanded by Benoit Paul Emile Clapeyronin in1834 and mathematically explored by Rudolf Clausius in 1857.

Carnot Engine Explained

Every thermodynamic system exists in a particular state at a point of time. A thermodynamic cycle occurs when a system is taken through a series of different states and finally returned to its initial state.

The system may perform some work on its surroundings, hence acting as a heat engine.

A heat engine transfers energy from a warm region to a cold region. In this process, some of that energy is converted into mechanical work.

In the above figure,
T_H – “hot” temperature (The temperature of hot reservoir).
T_C – “cold” temperature (The temperature of cold reservoir).
Q_H – Heat supplied by boiler or hot reservoir.
Q_C – Heat delivered by stream of cold water or cold reservoir.
W – Mechanical work by system on surroundings.

Here, the left side reservoir is called Source. It is used to supply Q_H.
And, the right side reservoir is called Sink. It is used to transfer heat Q_c.

In the above figure, the working body(system) can be any vapor or fluid body through which heat “Q” can be transmitted to yield work. 

Here, W denotes the movement of the piston as it is used to rotate a crank-arm(Thus the heat is converted into mechanical work).

Carnot’s Theorem

“No engine operating between two heat reservoirs can be more efficient than a Carnot engine operating between the same reservoirs.“

What is the Carnot Cycle?

A Carnot cycle is defined as an ideal reversible closed thermodynamic cycle in which there are four successive operations involved, which are isothermal expansion, adiabatic expansion, isothermal compression and adiabatic compression. 

During these operations, the expansion and compression of substance can be done up to the desired point and back to the initial state.

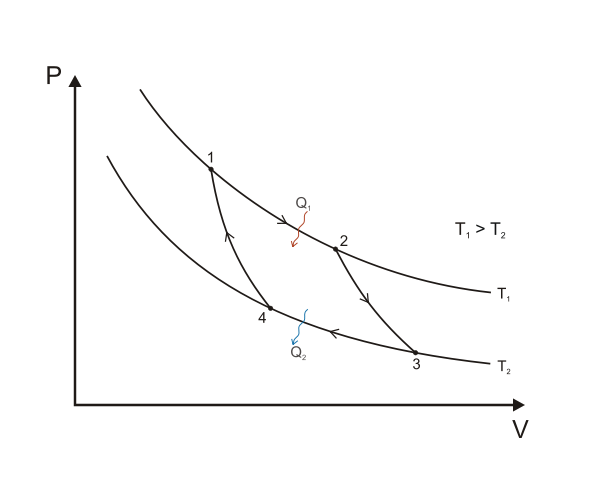
Work Done and Efficiency

The Carnot cycle when acting as a heat engine consists of the following 4 steps:

1. Reversible Isothermal Expansion: (Path 1 to 2 in the above figure, from P₁, V₁, T₁ to P₂, V₂, T₂) During this step, the gas is allowed to expand and do work on the surroundings. The “hot” temperature(\(T_H\)) of the gas is constant during this step. The expansion is isothermal. The gas expansion is propelled by absorption of heat energy \(Q_1\) and \(\Delta S_H = Q_H / T_H\) of entropy from the high temperature reservoir.
   \(\bf{W_{1 \rightarrow 2} = Q_1 = \mu \times r \times T_1 \times \ln(\frac{V_2}{V_1})}\)

2. Reversible Adiabatic(Isentropic) Expansion: (Path 2 to 3, from P₂, V₂, T₂ to P₃, V₃, T₂) For this process, the system is thermally insulated and the gas continues to expand and do work on its surroundings. The gas continues to expand, doing work on the surroundings, and losing an equivalent amount of internal energy. The gas expansion causes it to cool to the “cold” temperature, \(T-C\). The entropy remains unchanged.
   \(\bf{W_{2 \rightarrow 3} = \frac{\mu R}{\gamma -1} \times (T_1 – T_2)}\)

3. Reversible Isothermal Compression: (Path 3 to 4, from P₃, V₃, T₂ to P₄, V₄, T₂) Now the gas is exposed to the cold temperature reservoir while the surroundings do work on the gas by compressing it, while causing an amount of heat energy \(Q_2\) and of entropy \(\Delta S_C = Q_C / T_C\) to flow out of the gas to the low temperature reservoir. This work is less than the work performed on the surroundings in step 1 because it occurs at a lower pressure given the removal of heat to the cold reservoir as the compression occurs.
   \(\bf{W_{3 \rightarrow 4} = \mu \times r \times T_2 \times \ln(\frac{V_3}{V_4})}\)

4. Reversible Adiabatic(Isentropic) Compression: (Path 4 to 1, from P₄, V₄, T₂ to P₁, V₁, T₁) Once again the piston and cylinder are assumed to be thermally insulated and the cold temperature reservoir is removed. During this step, the surroundings continue to do work to further compress the gas and both the temperature and pressure rise now that the heat sink has been removed. This additional work increases the internal energy of the gas, compressing it and causing the temperature to rise to \(T_H\). The entropy remains unchanged. At this point the gas is in the same state as at the start of step 1.
   \(\bf{W_{4 \rightarrow 1} = \frac{\mu R}{\gamma -1} \times (T_1 – T_2)}\)

Hence, Total Work Done by the gas on its surroundings in one cycle is,

\(W = W_{1 \rightarrow 2} + W_{2 \rightarrow 3} + W_{3 \rightarrow 4} + W_{4 \rightarrow 1}\)

\(\fbox{$\large{W = \mu r T_1 \ln(\frac{v_2}{v_1}) – \mu r T_2 \ln(\frac{v_3}{v_4})}$}\)

And, Net Efficiency(\(\bf{\eta}\)) of the Carnot cycle is,

\(\mbox{Net Efficiency}(\eta) =\frac{\mbox{Net workdone by the gas}}{\mbox{Heat absorbed by the gas}}\)

\(\eta = \frac{W}{Q_1} = \frac{Q_2 – Q_1}{Q_1} = 1 – \frac{Q_2}{Q_1} = 1 – \frac{T_2}{T_1} \frac{\ln(\frac{v_3}{v_4})}{\ln(\frac{v_2}{v_1})}\)

Since process \(2 \rightarrow 3\) is an adiabatic process,

\(T_1 v_1^{\gamma -1} = T_2 v_3^{\gamma -1}\)
\(\frac{v_2}{v_3} = (\frac{T_2}{T_1})^{\frac{1}{\gamma -1}}\)

Similarly for process \(4 \rightarrow 1\),

\(\frac{v_1}{v_2} = (\frac{T_2}{T_1})^{\frac{1}{\gamma -1}}\)
Hence, \(\frac{v_2}{v_3} = \frac{v_1}{v_2}\)

This gives,
\(\fbox{$\large{\mbox{Net Efficiency}(\eta) = 1 – \frac{T_2}{T_1}}$}\)

Carnot Engine Examples

Question 1. What is the efficiency of a Carnot engine that operates between the two temperatures 240℃ and 20℃?

Solution. Given,

\(T_H\) = 240℃ = (240 + 273)K = 513K
\(T_L\) = 20℃ = (20 + 273)K = 293K

\(\eta = 1 -\frac{T_L}{T_H}\)
\(⇒ \eta = 1 – \frac{293}{513}\)

\(⇒ \eta ≈ 0.429\)

∴The efficiency of the engine is 42.9% 

Question 2. A heat engine with 75% efficiency does 50kJ of work per Carnot cycle. What is the heat rejected in each cycle?

Solution. Carnot efficiency = Work Done/Heat absorbed(\(Q_1\))

\(⇒ 0.75 = \frac{50}{Q_1}\)
\(⇒ Q_1 = \frac{200}{3}\)

As Work = \(Q_1 – Q_2\)

\(⇒ Q_2 = \frac{200}{3} – 50 = \frac{50}{3}\)
\(⇒ Q_2 = 16.6kJ\)

Hence the heat rejected by the system in each cycle will be 16.6kJ.

FAQs