At some point in our life, we might have wondered why an object, for example, coffee, tea, or boiled water, that was initially hot, had, after a while, cooled down. The explanation to this intriguing question is Newton’s Law of Cooling.
Index
History
Newton’s Law of Cooling was developed by Sir Isaac Newton in 1701. The law was not stated, as it is in the present form, initially. Newton noted that the rate of temperature change of a body is proportional to the difference in temperatures between the body and its surroundings. The law got its present form, after the confusion between the concepts of heat and temperature, much after 1701.

Newton’s Law of Cooling Explained
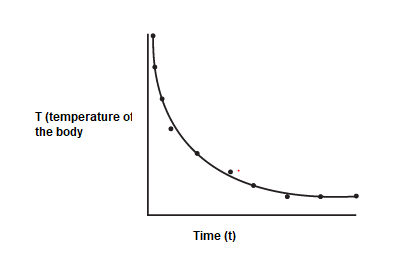
Statement: “The rate of heat loss of a body is directly proportional to the difference in the temperatures between the body and its surroundings.”
Newton’s law of cooling explains the rate at which an object/entity changes its temperature when it is exposed to radiation. This change is almost proportional to the difference between the object’s temperature and its surroundings’ temperature, given that this difference is quite small.
The formula of this law can be used to calculate how quickly a substance, at a particular temperature, would cool in a particular environment.
It also allows us to determine how the rate of cooling of an object depends not only on the temperature difference between the substance and the surrounding but also on the constant of the substance.
Formula
Newton’s Law of Cooling formula is expressed by,
\(T(t) = T_s + (T_0 – T_s)e^{-kt}\)Where,
\(T(t)\) – object’s temperature at time ‘t’ (a.k.a \(T_f\),
\(T_s\) – surrounding temperature,
\(T_0\) – the initial temperature of the body,
\(t\) – time,
\(k\) – constant of proportionality (depends on area and nature of the surface which is in contact with surroundings)
Derivation
According to Newton’s law of cooling,
\(\hspace{12pt} \frac{dT}{dt} ∝ (T – T_s)\)
\(⇒ \frac{dT}{dt} = -k (T – T_s)\)
The negative on the RHS implies that the rate of temperature change decreases.
Let \(T_f\) is the temperature at time t and \(T_0\) is the temperature at the beginning.
Applying Integration on both sides,
\(\hspace{12pt} \int_{T_f}^{T_0} \frac{dT}{(T – T_s)} = \int -k*dt\\
⇒ \ln((T_f – T_s) / (T_0 – T_s)) = -kt\\
⇒ (T_f – T_s) / (T_0 – T_s) = e^{-kt}\\
⇒ T_f – T_s = (T_0 – T_s)e^{-kt}\\
\)
\(∴ T_f = T_s + (T_0 – T_s)e^{-kt}\)
\(\hspace{30pt}\)OR
\(\hspace{10pt} T(t) = T_s + (T_0 – T_s)e^{-kt}\)
Limitations of Newton’s Law of Cooling
- The difference in temperatures between the surroundings and the object must be small,
- The loss of heat should be via radiation only,
- The temperature of the surroundings must remain constant during the cooling of the object.
Applications of Newton’s Law of Cooling
- Used to predict how long it will take for a hot object to cool down at a constant temperature.
- It also helps to indicate the death time given by the probable body temperature at the death time and the current body temperature.
Examples
Question 1. A body with a temperature of 40o C is kept in the surroundings with a constant temperature of 20o C. If the temperature falls to 35o C in 10 minutes, find out how much excess time it will take for the body to attain the temperature of 30o C.
Solution. The initial temperature of the body, \(T_0\) = 40o C.
Surroundings temperature, \(T_s\) = 20°C.
Temperature of body after 10 minutes, T(10) = 35°C
⇒ T(t) = T_s + (T_0 – T_s)e^{-kt}\\
⇒ 35 = 20 + (40 – 20)e^{-k.10}\\
⇒ e{-10k} = 3/4\\
⇒ k = \ln(4/3)/10 … (1)\\
\)
Now, for next interval,
\(\hspace{12pt} (30 – 20) = (35 – 20)e^{-kt}\\
⇒ e^{-kt} = 2/3\\
⇒ kt = \ln(3/2) … (2)\\
\)
From (1) and (2),
\(t = 10[ \ln(3/2) / \ln(4/3) ] = 14.096 min\)
Question 2. Water in a vessel is heated to 80o C for 10 minutes. How much would the temperature be, if k = 0.056 per minute and the surrounding temperature is 25o C?
Solution: Given,
\(T_s\) = 30o C
\(T_s\) = 100o C
\(t\) = 10 min
\(k\) = 0.056
Now, substituting the above data in Newton’s law of cooling formula,
\(⇒ T(t) = T_s + (T_0 – T_s)e^{-kt}\\
⇒ T(10) = 30 + (100 – 30)e^{-0.056*10}\\
⇒ T(10) = 30 + 70*0.57\\
∴ T(10) = 69.9°C\\
\)
∴ Temperature cools down from 100°C to 69.9°C after 10 minutes.
FAQs
The rate of cooling of a body is dependent of the nature of the surface of the body, the area of the body, the excess of temperature of the body above that of the surroundings and also on the temperature of the surroundings.
Yes, the two laws are related.
-Stefan’s law: The total radiant energy per second per unit surface area of a perfectly black body is always proportional to the 4th power of its absolute temperature.
-Newton’s Law of Cooling: The rate of loss of heat of a body, subjected to radiation, is directly proportional to the differences in temperature between the body and its surroundings, and the temperature difference is less.
Newton’s law can be derived from Stefan’s law. If the temperature difference is very less, Stefan’s law can be altered to Newton’s law.
