Millikan’s Oil Drop Experiment was an experiment performed by the American physicist Robert A. Millikan and Harvey Fletcher in 1909 to measure the electric charge of a single electron.
The Millikan’s oil-drop experiment took place in the Ryerson Physical Laboratory at the University of Chicago.

Index
Apparatus of Millikan’s Oil Drop Experiment
Millikan’s and Fletcher’s apparatus contain a parallel pair of horizontal metal plates. By applying a potential difference across the plates, a uniform electric field was created in the space between the plates.
A ring of insulator was used to hold the plates apart. Four holes are drilled into the ring, three for illumination by a bright light, and another one to allow viewing through a microscope.
A fine mist of oil droplets was sprayed into a chamber above the plates. This type of oil was usually used in a vacuum apparatus and was chosen because it had an extremely low vapour pressure. Ordinary oil would evaporate under the heat, causing the mass of the oil drop to change over the course of the experiment.
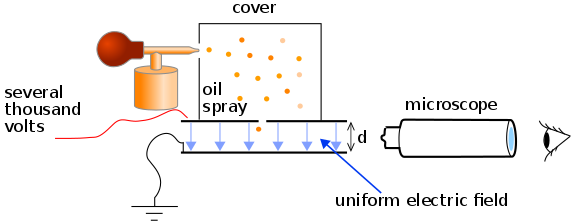
Millikan’s Oil Drop Experiment Procedure
Let us look at the procedure of the experiment.
- Oil is converted into tiny droplets using atomizer(spray). Those droplets pass through the holes present in the upper plate of the apparatus.
- The downward motions of droplets are observed through a microscope and then their terminal velocity is measured.
- The air inside the chamber is ionized by passing a beam of X-rays through it. The oil droplets acquire electric charge when they collide with gaseous ions produced by ionization of air.
- The electric field is set up between the two plates and so the motion of charged oil droplets can be controlled by the electric field.
- Gravity attracts the oil in a downward direction and the electric field pushes the charge upward. The strength of the electric field is regulated so that the oil droplet reaches an equilibrium position with gravity.
- The charge over the droplet is calculated at equilibrium, which is dependent on the strength of the electric field and mass of the droplet.
Millikan’s Oil Drop Experiment Calculation
Let us calculate the electron charge by using the method explained in this experiment.
Electron’s Charge is denoted by e,
Electric Field is denoted by E,
Droplet’s Mass is denoted by m,
Gravitational Acceleration is denoted by g
At Equilibrium,
\(F_{up} = F_{down}\\
F_{up} = e * E\\
F_{down} = mg\\
e * E = mg\\
e = mg / E\\
\)
We can see how an electron charge is measured by Millikan. Millikan found that all drops had charges that were 1.6x 10-19 C multiples.
Conclusion of Millikan’s Experiment
The charge over any oil droplet is always an integral value of e (1.6 x 10-19). Therefore, Millikan concluded that the charge is always quantified, i.e. the charge on any particle will always be an integral multiple of e.
Problems
Question. A tiny spherical oil drop carrying net charge q is balanced in still air with a vertical uniform electric field of strength \(\frac{81\pi}{7} * 10^5\) V/m (volts/meter). When the field is switched off, the drop is observed to fall with terminal velocity \(2 *10^{-3}\) m/s.
Given; g = \(9.8 m/s^2\), viscosity of the air = \(1.8×10^2 N⋅s/m^2\) and density of oil = \(900 kg/m^2\), the magnitude of q is,
- \(1.6×10^{−19} C\)
- \(3.2×10{−19} C\)
- \(4.8×10{−19} C\)
- \(8.0×10{−19} C\)
Solution. The forces acting on the oil drop are its weight, buoyant force, and electrostatic force. The buoyant force on the oil drop is very small as compared to the other two forces.
Let net Charge = q
g = \(9.8 m/s^2\) (Given)
Viscosity of the air = \(1.8×10^2 N⋅s/m^2\)(Given)
Terminal velocity= \(2 *10^{-3} m/s\) (Given)
Density of oil = \(900 kg/m^3\) (Given)
Thus, the weight of the spherical oil drop is balanced by electrostatic force,
\(qE = \frac{4}{3}πr^3\rho g\).
The drop attains terminal velocity in absence of electric field, when viscous force is equal to its weight i.e. ,
\(6 \pi \eta rv = \frac{4}{3} \pi r^3 \rho g\).
Eliminate r from above equations to get the charge,
\(q = \frac{4 \pi \rho g}{3E}(\frac{9 \rho v}{2 \rho g})^{3/2}\)
Substitute given parameters in the above equation to get, \(q = 8.0×10^{−19} C\).
FAQs
Paraffin oil
August 1913
The experiment with Millikan is important because it defines the charge on an electron. Millikan used a very basic, very subtle system in which the behavior of gravitational, electrical, and (air) drag forces were controlled.
