In combinatorics, the rule of product or multiplication principle is a basic counting principle, which here we know as the Fundamental Principle of Counting. It is a rule which we use to get the total number of possible outcomes as well as to find out different outcomes of the given situation.
Index
Statement
The fundamental counting principle or simply the multiplication principle states that “If there are x ways to do one thing, and y ways to do another thing, then there are x*y ways to do both things.”.
The counting principle can be extended to situations where you have more than 2 choices.
i.e “If there are x ways to do one thing, y ways to do the second thing and z ways to do the third thing, then there are x*y*z ways to do the three things.”
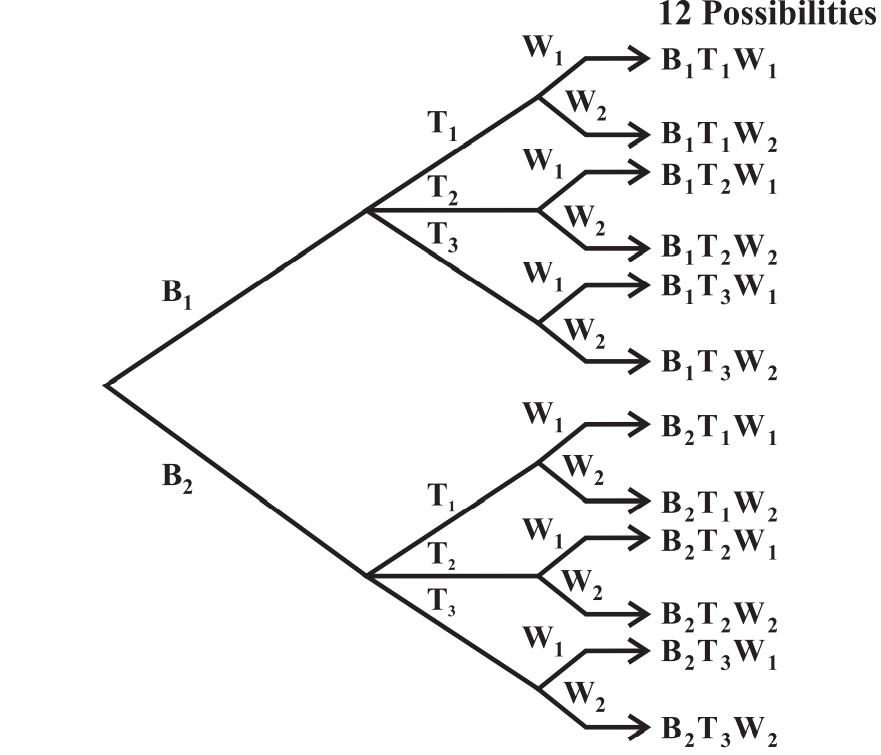
Example: If there are 2 Bags(B) & 3 Tiffin Boxes(T).
Let Bags be \(B_1 \text{ & } B_2\)
and Tiffin Boxes be \(T_1, T_2 \text{ & } T_3\)
Now total no. of possibilities of getting one bottle and one tiffin box is 2*3 = 6.
If we add 2 Water Bottles(W) i.e \(W_1 \text{ & } W_2\).
Now we have a total no. of possibilities as 6*2 = 12
Note: This principle is applicable only when the events and choices made are independent of each other. In the above example, you can observe that selecting a bag is independent of selecting a tiffin box, thus the principle is applicable.
Example: If the question says something like you can’t select \(i^{th}\) tiffin box when you select \(i^{th}\) bag, then this principle wouldn’t apply.
The total no. of possibilities of all events is also known as Sample Space.
Application
In Set Theory, this multiplication principle is often taken to be the definition of the product of cardinal numbers. We have
\(\displaystyle |S_{1}|\cdot |S_{2}|\cdots |S_{n}|=|S_{1}\times S_{2}\times \cdots \times S_{n}|\)Where \(\displaystyle \times\) is the Cartesian product operator. These sets need not be finite, nor is it necessary to have only finitely many factors in the product.
In Probability, as we go deeper with more complex questions, we use the Fundamental Principle of counting method with Permutations and Combinations to get the desired results.
Examples
Question 1. Given 5 flags of different colours, how many different signals can be generated if each signal requires the use of 2 flags, one below the other?
Solution. As two flags are to be arranged then
no. of possibilities for 1st flag would be 5.
Now as we have already picked one no. of flags left is 4
So for the 2nd flag no. of possibilities will be 4.
=> total no. of signals that can be generated using two flags will be = 5*4 = 20.
Question 2. How many 5-digit telephone numbers can be constructed using the digits 0 to 9 if each number starts with 67 and no digit appears more than once?
Solution. Here 1st two no.s are fixed i.e. 6,7
6 7 __ __ __
So now 3 more digits to be placed out of 8 leftover digits.
Thus, to fill the 3rd place there are 8 ways left, after fixing the 3rd place, for the 4th place we have 7 digits left, and so on for 5th, we have 6 digits.
=> no. of Telephone no. that can be formed are
= 1(no. 6 is fixed)* 1(no.7 is fixed) * 8(leftover 8)* 7(leftover 7)* 6(leftover 6)
= (1)*(1)*(8)*(7)*(6)
= 336.
FAQs
This counting method uses given data and simple multiplication we can find out all possible outcomes for the given event.
This counting method will be rigorously used in the upcoming work of Probability.
This formula at very basic is just making combinations with given data and constraints.
Mostly we will be sticking to Combinations but in some cases, we will also dig in the permutations.
