Brewster’s Law gives the exact angle of incidence for different materials and wavelengths of light for which the reflected ray is completely polarised. This angle of incidence is called the polarization angle or Brewster’s angle.
Index
History
Sir David Brewster was a Scottish physicist, inventor, author, and academic administrator, he is remembered by physicists for his work in optics especially on the polarization of light. He also invented two types of polarimeters. He was called the “father of modern experimental optics” and “the Johannes Kepler of optics”.

Brewster’s Law Explained
Let’s dive deep into the explanation of Brewster’s Law.
What is Brewster’s Law?
The Bruster’s law states that,
Maximum polarization of an unpolarized light ray occurs when its refractive index is equal to the tangent of the angle of incidence of the ray.
The refractive index of a particular material is different for different wavelengths of light, so the angle of incidence also depends on the wavelength of light used.
This law can be mathematically represented as,
\(\mu_r = \tan(\theta_i)\)
Here,
\(\mu_r\) is the relative refractive index of the material and its surrounding
\(\theta_i\) is the angle of incidence of the light ray
The angle of incidence obtained by Brewster’s Law is called Brewster’s angle or polarization angle.
The Brewster’s Law can also be stated as,
When the reflected and refracted rays are perpendicular to each other the light ray reflected off the refracting surface is completely polarized perpendicular to the refracting plane.
This second statement can be proved using the first one.
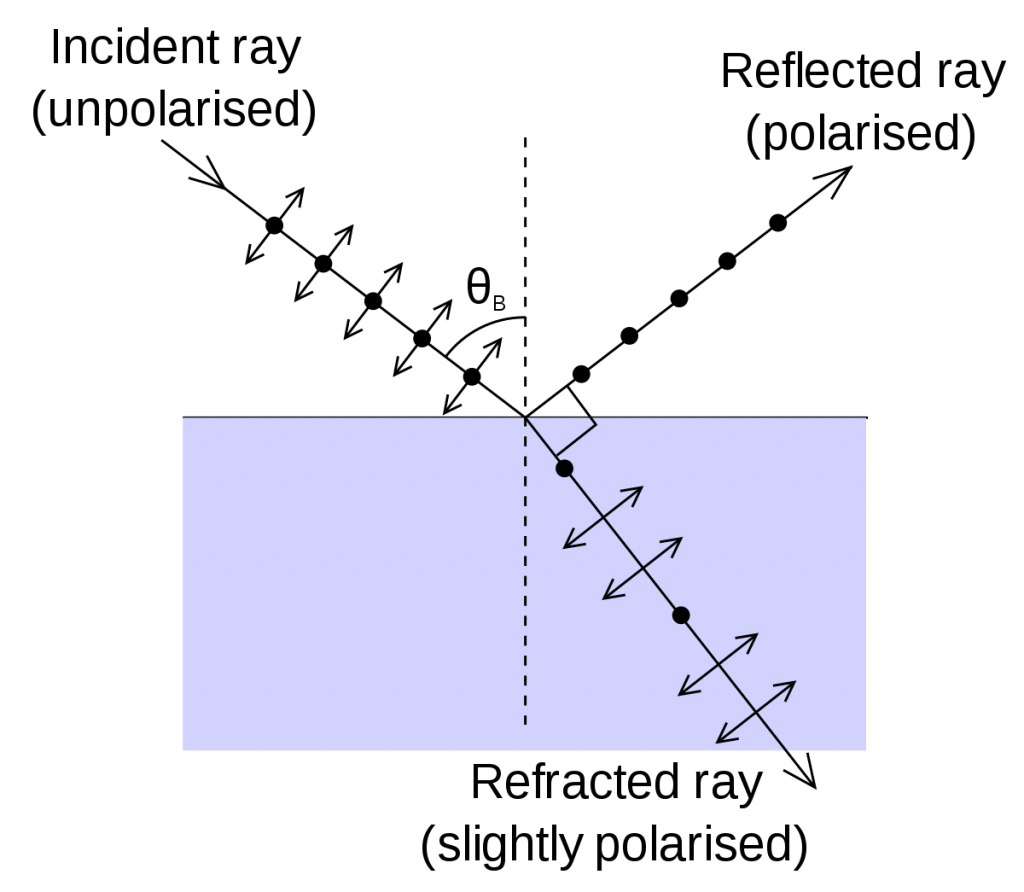
When the refracted and reflected rays are perpendicular to each other, then the component of light parallel to the refracting plane is cancelled out due to the direction of propagation of light which is in the same direction as this component of light. So, the component left is only the one perpendicular to the refracting plane.
Proof
Let us look at the proof of Brewster’s law.
\(\mu = \tan(\theta_i)\)
\(\mu = \frac{\sin(\theta_i)}{\cos(\theta_i)} … (1)\)
Form Snell’s law, we know that
\(\mu = \frac{\sin(\theta_i)}{\cos(\theta_r)} … (2)\) here, \(\theta_r\) is angle of refraction
Comparing (1) and (2)
\(\frac{\sin(\theta_i)}{\cos(\theta_r)} = \frac{\sin(\theta_i)}{\cos(\theta_i)}\)
=> \(\frac{1}{\cos(\theta_r)} = \frac{1}{\cos(\theta_i)}\)
=> \(\sin(\theta_r) = \cos(\theta_i)\)
We know that, \(\mbox{angle of incidence}(\theta_i) = \mbox{angle of reflection}(\theta_{re})\)
=> (\cos(\theta_i) = \cos(\theta_{re}))
=> \(\sin(\theta_r) = \cos(\theta_{re})\)
=> \(\sin(\theta_r) = \sin(90 – \theta_{re})\)
=> \(\theta_r = 90 – \theta_{re}\)
=> \(\theta_r + \theta_{re} = 90\)
The angle between refracting surface and reflected ray \((\alpha_{re}) = 90 – \theta_{re}\)
The angle between refracting surface and refracted ray \((\alpha_{r}) = 90 – \theta_{r}\)
So, \(\alpha_{re} + \alpha_r = 90 – \theta_{re} + 90 – \theta_r\)
=> \(\alpha_{re} + \alpha_r = 180 – (\theta_{re} + \theta_r)\)
=> \(\alpha_{re} + \alpha_r = 180 – 90\)
=> \(\alpha_{re} + \alpha_r = 90\)
Therefore, the angle between reflected ray and refracted ray is 90.
Relation Between Critical Angle and Brewster’s Angle
There is a relation between Brewster’s angle and critical angle of a material.
Brewster’s angle = \(\theta\)
Critical angle = \(\epsilon\)
\(\theta = \tan^{-1}(\mu_r)\)
=> \(\tan(\theta) = \mu_r … (1)\)
\(\epsilon = \sin^{-1}(1/\mu_r)\)
=> \(\sin(\epsilon) = 1/\mu_r … (2)\)
Using equation (1) in equation (2)
\(\tan(\theta) = 1/\sin(\epsilon)\)
\(\theta = \tan^{-1}(1/\sin(\epsilon))\)
Hence, Brewster’s angle can be found if the critical angle of a material is known through the above equation.
Applications of Brewster’s Law
- Used in polarized sunglasses reduce the glare of reflected sunlight.
- Used in polarizing filter of the camera allows photographers to take pictures of objects below the water surface.
- Used in recording a hologram.
- Used in microscopes for air-liquid interfaces, where the molecule layers shine but the liquid appears black making them presentable.
- To allow a gas laser to leave the laser tube a window tilted at Brewster’s angle is used.
Brewster’s Law Examples
Question 1. Calculate the angle of incidence for a light ray travelling from glass with a refractive index(\(\mu_g\)) of 1.5 to a material of refractive index(\(\mu_m\)) 2, for which the ray of light reflected off the surface of the material during refraction, is completely polarized.
Answer. According to Brewster’s law, the reflected part of the light is completely polarized when the tangent of the incident ray is equal to the refractive index of the material. So,
\(\mu_ r = \tan(\theta_i)\)
=> \(\frac{2}{1.5} = \tan(\theta_i)\)
=> \(\tan^{-1}(1.33) = \theta_i\)
=> \(\theta_i = 53.06^{\circ}\)
So, the angle of incidence for which the ray reflected part of light is completely polarized in this experiment is \(53.06^{\circ}\). This angle is also known as Brewster’s angle.
Question 2. If a light ray at the surface of water is both refracted and reflected. Then calculate the angle of refraction of the light ray for which, this and the angle of reflection are perpendicular to each other (refractive index of water (\(\mu\)) = 1.333).
Answer. Given, the refractive index of water(\(\mu\)) = 1.333
We can calculate the angle of incidence for this situation using Brewster’s Law.
\(\mu_ r = \tan(\theta_i)\)
=> \(1.333 = \tan(\theta_i)\)
=> \(\tan^{-1}(1.333) = \theta_i\)
=>\(\theta_i = 53.12^{\circ}\)
So, the angle of incidence(\(\theta_i\)) = \(53.12^{\circ}\)
From the laws of reflection,
\(\mbox{angle of reflection}(\theta_{re}) = \mbox{angle of incidence}(\theta_i)\)
So, the angle of reflection of the light ray\((\theta_{re}) = 53.12^{\circ}\)
We know that the angle between refracted ray reflected ray is \(90^{\circ}\).
And we also know that the sum of angle of reflection, refraction and the angle between the refracted ray and reflected ray is \(180^{\circ}\), as it is the angle between normals.
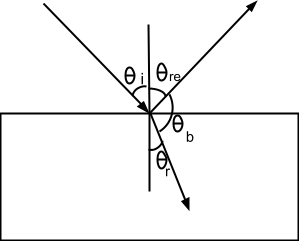
Here, \(\theta_b\) is the angle between incident ray and reflected ray.
So, \(\theta_{re} + \theta_b + \theta_r = 180\)
As we know that \(\theta_b = 90\) from Brewster’s Law
\(\theta_{re} + 90 + \theta_r = 180\)
\(\theta_{re} + \theta_r = 90\)
\(53.12 + \theta_r = 90\)
\(\theta_r = 36.88^{\circ}\)
Therefore, the required angle of refraction is \(36.88^{\circ}\).
FAQs
It is a law that gives the relation to find the angle of incidence of a light ray, for which the reflected part of the ray is completely polarized. The mathematical equation of this law is,
\(\mu_r = \tan(\theta_i)\)
Here,
\(r\) is the relative refractive index of the material with respect to the medium.
\(i\) is the angle of incidence of the light ray on the refracting medium.
The angle of incidence at which the reflected part of the ray is completely polarized perpendicular to the refracting surface.
Brewster angle prism is used in laser physics for bending and directing polarized lasers without any reflective loss in their intensity.
No, intensity of the polarized light ray decreases because some part of the incident light ray is refracted also, which is not completely polarized though and has both the perpendicular and parallel components of light.
