Biconvex lens is composed of two spherical surfaces of glass-air interfaces. The two circular surfaces are convex, or bulging out, hence the name biconvex lens.
Index
History
The first evidence of any reference of a lens dates back to 442 B.C. Aristophanes, in his play The Clouds, mentions a burning-glass which probably was a biconvex lens. Lenses were extensively used in spectacles in the 13th century. The optical microscope was invented in 1595 A.D. The refracting telescope was invented in 1605. Since these two inventions the importance of lenses and optics, in general, has achieved new heights.
Construction and Lens Maker’s Formula
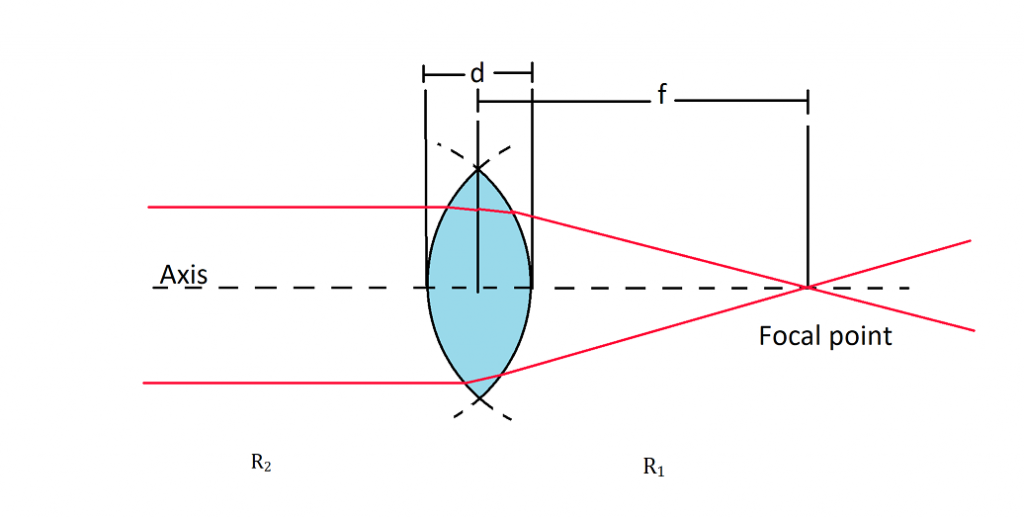
To construct any lens, data about the radii of spherical surfaces need to be known. A biconvex lens has two convex(outwards bulging) surfaces. The line joining the center of the two spherical surfaces should pass through the actual geometrical center of the lens.
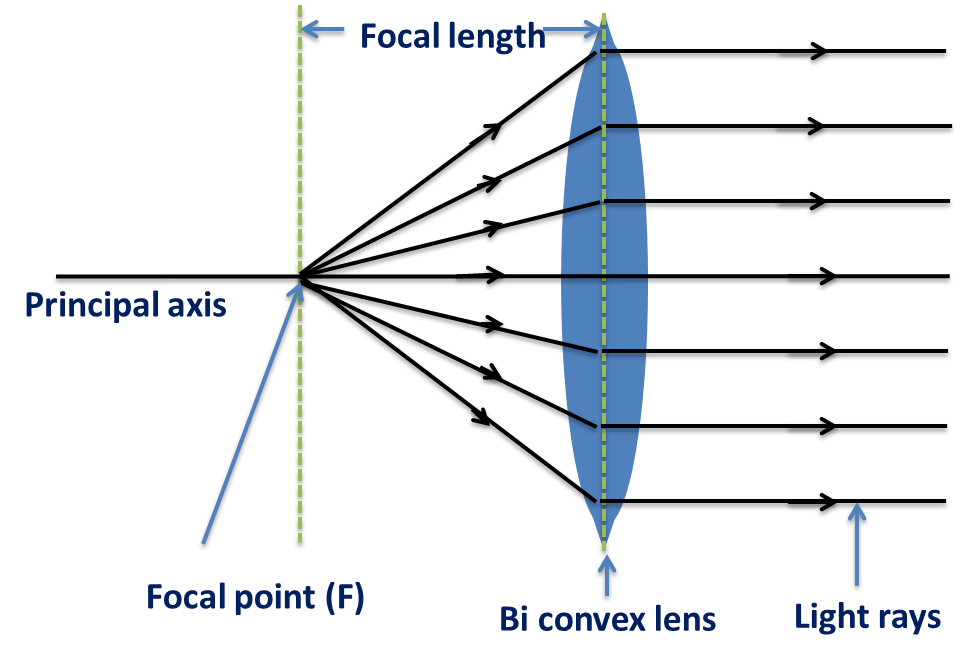
In order to construct a convex lens with a specific focal length, the lens maker’s formula is used.
The Lens Maker’s Formula:
\(\frac{1}{f}=(n-1)\left[\frac{1}{R_{1}}-\frac{1}{R_{2}}+\frac{(n-1) d}{n R_{1} R_{2}}\right]\)where,
\(f\) → Focal Length
\(n\) → Refractive Index
\(R_{1}\) → Radius of curvature of surface 1
\(R_{2}\) → Radius of curvature of surface 2
\(d\) → Thickness of the lens.
If \(d << R_{1}R_{2}\),
\(\frac{1}{f}=(n-1)\left[\frac{1}{R_{1}}-\frac{1}{R_{2}}\right]\)
Know more on Lens Maker’s Formula
The Biconvex Lens Formula
We need to find a relation between focal length, object distance, and image distance for a convex lens.
We know that, refraction at any spherical surface is given by:
\(\frac{\mu_{2}}{v}-\frac{\mu_{1}}{u}=\frac{\mu_{2}-\mu_{1}}{R}\)
For surface 1:
\(\frac{\mu_{2}}{v’}-\frac{\mu_{1}}{u}=\frac{\mu_{2}-\mu_{1}}{R_{1}} … (1)\)
For surface 2, the virtual image formed by surface 1 serves as object for surface 2,
\(\frac{\mu_{1}}{v}-\frac{\mu_{2}}{v’}=\frac{\mu_{2}-\mu_{1}}{-R_{2}} … (2)\)
Negative sign on R because the centre of the spherical surface is on the left side.
Adding equations (1) and (2) and rearranging gives,
\(\frac{1}{v}-\frac{1}{u}=(n-1)\left[\frac{1}{R_{1}}-\frac{1}{R_{2}}\right]\)
But this is also equal to \(\frac{1}{f}\).
Therefore,
\(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)
Various Modes of working of Biconvex Lens
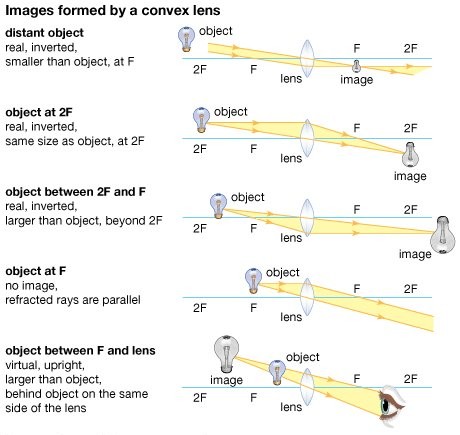
Case 1: Object at infinity (Distant Object):
\(u = -\inf\)
\(v = +F\)
The image formed is real, inverted, and smaller than the object.
Uses: Used in-camera to form an image on the sensor.
Case 2: Object at 2F:
\(u = -2F\)
\(v = 2F\)
The image formed is real, inverted, and has the same size as the original.
Uses: Used in telescopes to invert the image.
Case 3: Object between 2F and F:
\(F \leq u \leq 2F\)
\(2F \leq v \leq \inf\)
The image formed is real, inverted, and magnified.
Uses: This type of setup is used in projectors.
Case 4: Object at F:
\(u = F\)
\(v → \inf\)
The image formed is at infinity or no image is formed.
Uses: This type of setup is used in flashlights, spotlights, and Floodlights.
Case 5: Object between F and the Center of the lens:
\(0 \leq u \leq F\)
\(v = \text{beyond the object}\)
The image formed is virtual, upright, magnified, and on the same side as that of the object.
FAQs
The magnification factor is defined as,
\(M = \frac{v}{u}\)
where, v → distance of image
u → distance of the object
The sign convention is made clear with the help of a figure (Source):![]()
Biconvex lens is a simple lens, it comprising two spherical convex surfaces, normally with the same radius of curvature.
The main difference between the biconvex & biconcave lens is that the biconcave is thinner in the middle than the outer and the biconvex is thicker at the center than the outer rim.
Related Topic