The secant method is a root-finding algorithm, used in numerical analysis. It is a recursive method for finding the root of polynomials by successive approximation.
Index
Secant Method Explained
Let us understand this root-finding algorithm by looking at the general formula, its derivation and then the algorithm which helps in solving any root-finding problems.
Secant Method Formula
The general secant method formula is defined as follows:
\(\large{x_n = x_{n – 1} – f(x_n – 1)\frac{x_{n – 1} – x_{n – 2}}{f(x_{n – 1}) – f(x_{n – 2})} = \frac{x_{n – 2}f(x_{n – 1}) – x_{n – 1}f(x_{n – 2})}{f(x_{n – 1}) – f(x_{n – 2})}}\)For the above recurrence relation, two initial values, \(x_0\) and \(x_1\) are required.
Derivation
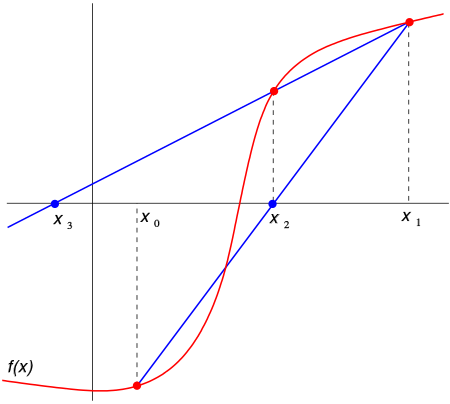
Using the initial values \(x_0\) and \(x_1\), a line is constructed through the points \((x_0, f(x_0))\) and \((x_1, f(x_1))\), as shown in the above figure.
The equation of this line in slope-intercept from is
\(y = \frac{f(x_1) – f(x_0)}{x_1 – x_0} (x_1 – x_0) + f(x_1)\)
The root of the above equation, when y = 0, is
\(x = x_1 – f(x_1)\frac{x_1 – x_0}{f(x_1) – f(x_0)}\)
This \(x\) is then used as \(x_2\) for the next iteration and \(x_1\) and \(x_2\) are used instead of \(x_0\) and \(x_1\). This process is continued until a high level of precision is reached.
\(x_2 = x_1 – f(x_1)\frac{x_1 – x_0}{f(x_1) – f(x_0)}\)
\(x_3 = x_2 – f(x_2)\frac{x_2 – x_1}{f(x_2) – f(x_1)}\)
.
.
\(x_n = x_{n-1} – f(x_{n-1})\frac{x_{n-1} – x_{n-2}}{f(x_{n-1}) – f(x_{n-2})}\)
The iterations of this method converge to a root of \(f\), if the initial values \(x_0\) and \(x_1\) are sufficiently close to the root.
Algorithm
The algorithm of secant method is as follows:
- Start.
- Get values of \(x_0\), \(x_1\) and \(e\), where \(e\) is the stopping criteria.
- Compute \(f(x_0)\) and \(f(x_1)\).
- Compute \(x_2 = x_1 – f(x_1)\frac{x_1 – x_0}{f(x_1) – f(x_0)}\)
- Test for accuracy of \(x_2\),
\(\,\,\,\,\)If \(\left| \frac{x_2 – x_1}{x_2} \right| \gt e\)
\(\,\,\,\,\)Then \(x_0 = x_1\)& \(x_1 = x_2\)
\(\,\,\,\,\,\,\,\,\)goto Step 4
\(\,\,\,\,\)Else
\(\,\,\,\,\,\,\,\,\)goto Step 6 - Display required root.
- Stop.
Advantages of the Method
- The rate of convergence of secant method is faster compared to Bisection method or Regula Falsi method.
- This method uses the two most recent approximations of root to find new approximations, instead of using only the approximations that bound the interval to enclose root.
Disadvantages of the Method
The disadvantage of this method is that convergence is not always assured. So, the number of iterations used must be limited, when implemented on the computer
Secant Method Example
Question. Compute the root of \(x^2 e^{-x/2}-1 = 0\) in the interval [0, 2] using the secant method. The root should be correct to three decimal places. The initial values are 1.42 and 1.43.
Solution. Given that,
\(f(x) = x^2 e^{-x/2}-1\)
\(x_0 = 1.42\)
\(x_1 = 1.43\)
\(f(x_0) = (1.42)^2 e^{(-1.42/2)} – 1 = -0.0086\)
\(f(x_1) = 0.00034\)
On applying the general formula, we get,
First approx.:
\(x_2 = x_1 – f(x_1)\frac{x_1 – x_0}{f(x_1) – f(x_0)}\)
\(x_2 = 1.42 – f(1.43)\frac{1.43 – 1.42}{f(1.43) – f(1.42)}\)
\(x_2 = 1.4296\)
\(f(x_2) = f(1.4296) = -0.000011\)
2nd approx.:
\(x_3 = x_2 – f(x_2)\frac{x_2 – x_1}{f(x_2) – f(x_1)}\)
\(x_3 = 1.4296 – f(1.4296)\frac{1.4296 – 1.43}{f(1.4296) – f(1.43)}\)
\(x_3 = 1.4293\)
∴ As \(x_2\) and \(x_3\) match upto three decimal places, the required root is 1.429.
Related Article: Newton Raphson Method
FAQs
The secant method is an algorithm used to find the root of a polynomial, in numerical analysis.
The general formula for this method of root-finding is:
\(x_n = x_{n-1} – f(x_{n-1})\frac{x_{n-1} – x_{n-2}}{f(x_{n-1}) – f(x_{n-2})}\)
The disadvantage of this method is that convergence to the root of the polynomial is not guaranteed, so the number of iterations used must be limited, when implemented on the computer.
