Newton Raphson Method, also known as Newton’s Method, is a root-finding algorithm that produces successively better approximations to the roots of a real-valued fraction.
Index
Newton Raphson Method Explained
Let us understand this root-finding algorithm by looking at the general formula, its derivation and then the algorithm which helps in solving any root-finding problems.
Newton Raphson Method Formula
This method was named after Sir Isaac Newton and Joseph Raphson. It begins with a function \(f\) defined over real numbers, its derivative \(f’\), and an initial guess \(x_0\) for the root of \(f\).
The solution comes to a stop when the function satisfies the assumptions made in the derivation of the formula and the initial guess is close.
The General Newton Raphson Method Formula is:
\(\large{x_{n + 1} = x_n – \frac{f(x_n)}{f'(x_n)}}\)
The above formula is repeated until a sufficiently precise value is obtained.
Derivation
Consider, \(f : (a, b) \rightarrow \mathbb{R}\), a differentiable function defined on the interval \((a, b)\) with values in real numbers \(\mathbb{R}\), and some current approximation \(x_n\).
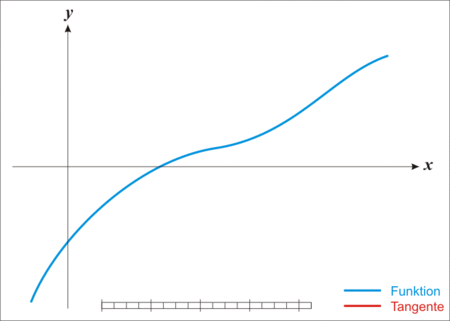
This function, \(f\) is represented by the blue curve in the above figure. The equation of a tangent to the curve \(y = f(x)\) at \(x = x_n\) is
\(y = f'(x_n)(x – x_n) + f(x_n)\)
Where, \(f’\) denotes the derivative.
The x-intercept of this tangent is taken as the next approximation, \(x_{n + 1}\), to the root, so that the equation of the tangent line is satisfied when \((x, y) = (x_{n + 1}, 0)\):
\(0 = f'(x_n)(x_{n + 1}- x_n) + f(x_n)\)
\(∴ x_{n + 1} = x_n – \frac{f(x_n)}{f'(x_n)}\)
The method usually converges, given that the initial guess is close enough to the unknown zero and that \(f’(x_0) \neq 0\).
Algorithm
- Compute the values of \(f(x)\) and \(f’(x)\) for a given initial \(x\).
- While the ratio of \(f(x)\) and \(f’(x)\) is greater than allowed error \(\epsilon\),
\(\,\,\,\,x_{n + 1} = x_n – \frac{f(x_n)}{f'(x_n)}\)
\(\,\,\,\,\)For all values from \(0\) to \(n\)
Advantages of the Method
- This root-finding method is the best method to solve non-linear equations.
- The method can also be used to solve non-linear differential and non-linear integral equations.
- The order of convergence is quadratic, faster compared to other methods.
- It is a simple method that can be easily implemented on a computer.
Disadvantages of the Method
- This method gets complicated if the derivative is not simple.
- The approximation must be chosen with great and sensitive attention.
- Sometimes, due to the assumptions made, the method may not converge.
- If the first derivative of the given function is not well-behaved in the neighborhood of a particular root, the method may overshoot and diverge from the root.
- If the method encounters a stationary point of the function, the derivative becomes 0, and the method will terminate.
Applications
- This method is used to find a minimum or maximum of a function.
- The method also finds application in finding multiplicative inverses of numbers and power series.
- It is used in solving transcendental equations, obtaining zeros of special functions such as Bessel functions.
- The method is used for the numerical verification for solutions of non-linear equations.
Newton Raphson Method Example
Question. Compute the root of \(f(x) = x^2 – 2\) with an initial guess \(x_0 = 2\). Begin with \(x_0\) and compute \(x_1\).
Solution. Given that,
\(f(x) = x^2 – 2\)
\(f'(x) = 2x\)
\(x_0 = 2\)
The sequence given by this method is:
\(\begin{array}
\, x_1 & = x_0 – \frac{f(x_0)}{f'(x_0)}\\
& = 2 – \frac{(2)^2 – 2}{2(2)}\\
& = 2 – \frac{1}{2}\\
x_1 & = \frac{3}{2}\\
\end{array}
\)
FAQs
The general formula for the Newton-Raphson method is:
\(x_1 = x_0 – \frac{f(x_0)}{f'(x_0)}\)
The Newton-Raphson method will fail in cases where the derivative is zero. When the derivative is close to zero, the tangent line is nearly horizontal and hence may overshoot the desired root.
The points at which the Newton-Raphson method fails are known as stationary points. A stationary point of a function f(x) is a point where its derivative is equal to 0.
More on Root Finding Methods:
