Curie’s Law

Curie Law is a law in magnetization that establishes a relation between the magnetic susceptibility and the magnetisation of a paramagnetic material.

A paramagnetic material is a metal that is weakly attracted to magnets.

The relation was experimentally discovered by a French physicist, Pierre Curie.

Statement

Statement of Curie Law: “The magnetization of a paramagnetic material is directly proportional to an applied magnetic field and inversely proportional to temperature, for large temperatures, weak magnetic fields.“

Curie Law Formula

The formula or the equation of Curie’s law is as follows:

\(M = \chi H\), with \(\chi = \frac{C}{T}\)

(After Curie’s temperature, \( \chi = \frac{c^{‘}}{T – T_{C}}\), where \(T_{C}\) is Curie’s temperature and \(c^{‘}\) is a constant)

Where,
? > 0 – Magnetic Susceptibility,
M – Magnitude of magnetization(amperes per meter, A/m),
H – Magnitude of the applied magnetic field(A/m),
T – Absolute temperature(kelvins, K),
C – Material specific Curie constant(k)

The formula or the relation holds only for high temperatures or weak magnetic fields.

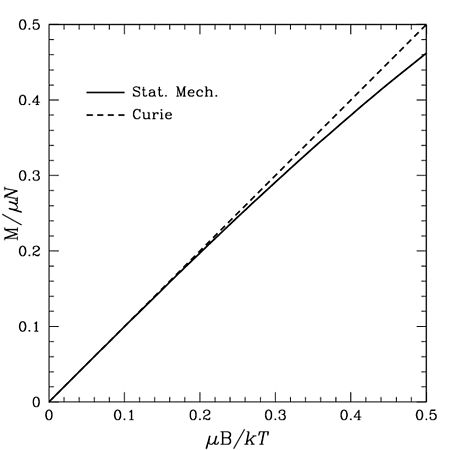
The statement doesn’t hold for all cases.

Example of Curie Law

Question. A toroid has a mean radius R equal to 20/π cm, and a total of 400 turns of wire carrying a current of 2.0A. An aluminium ring at temperature 280 K inside the toroid provides the core. 

(a) If the magnetization I is 4.8×10^-2 Am^-1, find the susceptibility of aluminium at 280 K.

 (b) If the temperature of the aluminium ring is raised to 320 K, what will be the magnetization?

Solution.

(a) The number of turns per unit length of the toroid is 
\(n = \frac{400}{2?R}\) 

The magnetic intensity H in the core is
\(H = ni = \frac{400 * 2.0A}{2?*\frac{20}{?}*10^{-2}m} = 2000 A m^{-1}\)

The susceptibility is 
\(\chi = I/H\)
\(∴ \chi = \frac{4.8*10^{-2}A m^{-1}}{2000 A m^{-1}} = 2.4*10^{-5}\)

(b) The susceptibility \(\chi\) of a paramagnetic substance varies with absolute temperature as \(\chi = c/T\).

 Thus, \(\chi_2/\chi_1 = T_1/T_2\)

The susceptibility of aluminium at temperature 320 K is, therefore, 
\(\chi = \frac{280}{320}*2.4*10^{-5} = 2.1*10^{-5}\)

Thus, the magnetization at 320 K is
\(I = \chi H = 2.1*10^{-5}*2000 A m^{-1}\)
\(∴ I = 4.2*10^{-5}Am^{-1}\)

FAQs