The Rectilinear Motion also called Linear motion is the uni-direction motion along a straight path. The direction of the motion is the direction in which velocity remains constant that is the objects move along the same axis and do not change their direction.
So, let us see the important formulas related to Rectilinear motion which will help you prepare for competitive examinations like JEE and NEET.
Index
Formulae
The Formulas related to Rectilinear Motion are as follows :
Average Velocity (in an interval) :
\( V_{av} = \bar{V} = \frac{Total\;displacement}{Total\;time\;taken}\) \(= \frac{ \vec{r_{f}}-\vec{r_{i}}}{ \Delta t}\)Average Speed (in an interval)
Average Speed \(= \frac{Total\;distance\;travelled }{Total\;time\;taken}\)
Instantaneous Velocity (at an instant) :
\(\vec {V_{inst}}= lim [\frac{\Delta \vec {r}}{\Delta t}]\)Average acceleration (in an interval):
\(\overrightarrow {a}_{av}= [\frac{\Delta \overrightarrow{V}}{\Delta t} =\frac{ \vec{V_{f}}-\vec{V_{i}}}{ \Delta t}\)Instantaneous Acceleration (at an instant):
\(\vec{v}_{inst}=\lim_{\Delta t\rightarrow 0}\left ( \frac{\Delta \vec{r}}{\Delta t} \right )\)Average acceleration (in an interval):
\(\vec{a}_{av}=\frac{\Delta \vec{r}}{\Delta t}=\frac{\vec{v_{f}}-\vec{v_{i}}}{\Delta t}\)Instantaneous Acceleration (at an instant):
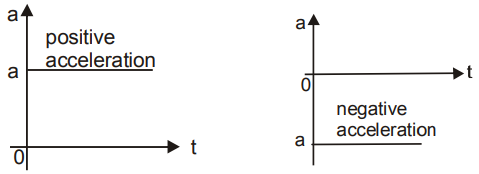
\(\vec{a}=\frac{d\vec{v}}{dt}=\lim_{\Delta t\rightarrow 0}\left ( \frac{\vec{\Delta v}}{\Delta t} \right )\)Graphs in Uniformly Accelerated Motion Along a Straight Line (a \(\neq\) 0)
- x is a quadratic polynomial in terms of t. Hence x – t graph is a parabola.

- v is a linear polynomial in terms of t. Hence v -t graph is a straight line of slope a.
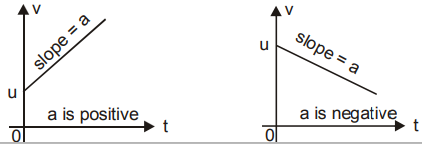
- a- t graph is a horizontal line because a is constant.
Maxima & Minima
\( \frac{dy}{dx} = 0\) & \(\frac{d}{dx} [\frac{dy}{dx}] < 0 \) at maximum
\(\frac{dy}{dx} = 0 \) & \(\frac{d}{dx}[\frac{dy}{dx}] > 0 \) at minima.
Equations of Motion (for Constant Acceleration a)
Following are the equations of motion in the case of constant acceleration also called as Kinematic equations.
(a) v = u + at
(b) \(s = ut + \frac{1}{2} at^{2} \,\,\,\)
c) \(v^{2} = u^{2} + 2 as\)
d) \(s = \frac{(u+v)}{2}t\)
e)\( s_{n} = u + \frac{a}{2} (2n -1)\)
For freely Falling Bodies : (u = 0)
(taking upward direction as positive)
(a) v = – gt
(b)\( s = – \frac{1}{2} gt^{2} \;\;\;\; s =vt + \frac{1}{2} gt^{2} \;\;\;\; h_{f} = h_{i} – \frac{1}{2}gt^{2}\)
(c)\(v^{2} = -2gs\)
(d)\(S_{n}= -\frac{g}{2} (2n -1)\).
So, those were all the important formulas related to Rectilinear Motion.
