Newton’s universal law of gravitation establishes a relationship between every particle and every other particle in the universe.
The publication of the theory is called the “First Great Unification”, as it marked the unification of the phenomena of gravity with known astronomical behaviours.
Index
History
Newton’s Law of Gravitation was formulated by Sir Isaac Newton in 1687 and used to explain the motions of the planets and their respective moons, which later had been reduced to a mathematical formula by Johannes Kepler in the early 17th century.

The Newton’s Law of Gravitation
Newton’s law of gravitation states that,
“Every particle attracts every other particle in the universe with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centres.”
So, what actually is gravitation? Gravitation is the force that pulls or attracts any two bodies to each other. Every object in this universe attracts every other object, except that in most cases, this force of attraction is very weak. This can be attributed to the large distance of separation between the objects.
A very common example of gravitation is human beings being able to stand on earth, instead of floating in the air. The earth has a substantial gravitational force. This force of gravity causes an acceleration due to gravity of approximately 9.8 m/s2.
Gravitational Force Formula
The gravitational force is proportional to the product of the masses of the two objects and inversely proportional to the square of the distance separating the two objects.
Mathematically gravitational force formula is noted as,
\(F = G \frac{m_1 m_2}{r^2}\)Where,
\(F\) – Gravitational force between the two bodies, measured in Newton(\(N\))
\(G \) – Universal Gravitational constant, \(\text{Value} = 6.674 \times 10^{-11} N m^2 kg^{-2}\)
\(m_1\) – Mass of 1st object measured in kilograms(kg)
\(m_2\) – Mass of 2nd object measured in kilograms(kg)
\(r\) – Distance between the center of masses of both bodies, measured in meter(km).
Out of the two masses, the heavier one is called source mass and the other is called test mass.
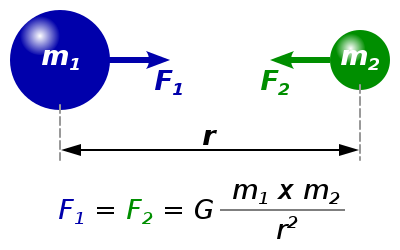
Newton’s universal law of gravitation possesses a resemblance with Coulomb’s Law of Electric Forces, which is used to calculate the magnitude of the electric force between two charged bodies.
Know More on Gravitation Formulas
Derivation
Let us consider a test mass(\(m\)), revolving around a source mass(\(M\)) in a circuit orbit of radius \(r\), with a constant angular speed(\(\omega\)).
The centripetal force acting on the test mass is,
\(F = mr \omega^2 = mr * \left(\frac{2\pi}{T}\right)^2\)
According to Kepler’s 3rd law,
\(T^2 \propto r^3\)
Know More on Kepler’s Law
Using this equation in the centripetal force equation,
\(F = \frac{4 \pi mr}{Kr^3}\), where \(K = \frac{4 \pi^2}{GM}\)
\(∴ F = \frac{GMm}{r^2}\)
Vector Representation
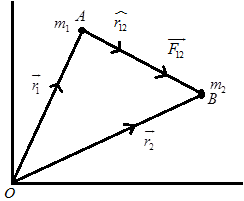
It can be deduced from the above figure that,
\(\overrightarrow{r_{12}} = (\overrightarrow{r_{1}} – \overrightarrow{r_{2}})\)
As we know,
\(\hat{r_{21}} = -\hat{r_{12}}\) → Eq(1)
It can be seen that the direction of the vector is from \(m_1\) to \(m_2\).
The force of attraction applied on \(m_2\) by \(m_1\) is,
\(\overrightarrow{F_{21}} = -\frac{G m_1 m_2}{r_{21}^2} \overrightarrow{r_{21}}\)
Similarily,
\(\overrightarrow{F_{12}} = -\frac{G m_1 m_2}{r_{12}^2} \overrightarrow{r_{12}}\) → Eq(2)
From Eq(1) and Eq(2),
\(\overrightarrow{F_{12}} = -\frac{G m_1 m_2}{(-r_{21})^2}(-\hat{r_{21}})\)
\(\Rightarrow \overrightarrow{F_{12}} = \frac{G m_1 m_2}{(r_{21})^2}(\hat{r_{21}})\)
\(∴ \overrightarrow{F_{12}} = – \overrightarrow{F_{21}}\)
Hence, the applied forces are equal and opposite. This shows that the gravitational force follows Newton’s third law.
Applications of Newton’s Law of Gravitation
- Newton’s law of gravitation helps in the prediction of the orbits and time periods of modern artificial satellites.
- This law determines the downward force on the surface of the earth.
- The law of gravity is used to calculate the force of attraction between two particles or objects.
- It is used to calculate the value of gravitational acceleration ‘g’ above the surface of Earth.
Solved Examples
Question. What is the gravitational force on an object of mass 300kg at the Earth’s surface?
Solution. Given data we have so far,
Mass of Earth(\(M\)) = 5.98 * 1024 kg
Mass of object(\(m\)) = 300 kg
Radius of Earth(\(r\)) = 6.38 * 106 m
Acceleration due to gravity(\(g\)) = 9.8 m/s2
Gravitational constant(\(G\)) = 6.67 * 10-11 Nm2/kg2
As we know from Newton’s law of gravitation formula,
\(\begin{align}
F & = G \frac{m_1 m_2}{r^2} \\
& = \frac{(6.67 * 10^{-11})(5.98 * 10^{24})(3 * 10^2)}{(6.38 * 10^6)^2} \\
& = \frac{119.7 * 10^{15}}{4.07044 * 10^{13}} \\
∴ F & = 2.94 * 10^3 \, N
\end{align}
\)
FAQs
Newton’s law of gravitation states that every particle attracts every other particle in the universe with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centres.
The value of the acceleration due to gravity, g, on Earth is 9.8 m/s2.
The mathematical formula for gravitational force is,
\(F = G \frac{m_1 m_2}{r^2}\)
Where,
\(F\) – Gravitational force between the two bodies, measured in Newton(\(N\))
\(G \) – Gravitational constant, \(\text{Value} = 6.674 \times 10^{-11} N m^2 kg^{-2}\)
\(m_1\) – Mass of 1st object measured in kilograms(kg)
\(m_2\) – Mass of 2nd object measured in kilograms(kg)
\(r\) – Distance between the center of masses of both bodies, measured in kilometer(km).
