Gravitation is a force that attracts every body with mass or energy in the universe towards every other body. Gravitation was first theorized by Sir Isaac Newton. In this article, we will see some important gravitation formulas which will also help you in preparation for competitive exams like JEE and NEET.
Index
Universal Law of Gravitation
The universal law of gravitation is represented as
\(F\propto \frac{m_{1}m_{2}}{r^{2}}\;or\;\;F=G\frac{m_{1}m_{2}}{r^{2}}\)where,
G = 6.67 × 10–11 Nm2kg–2 is the universal gravitational constant.
m1, m2 are the mass of two objects
r is the distance between the two objects
Know about Sir Isaac Newton
Newton’s Law of Gravitation in Vector Form
The vector form of law of gravitation is,
\(\overrightarrow{F}_{12}=\frac{Gm_{1}m_{2}}{r^{2}}\hat{r}_{12}\;\;\&\;\;\overrightarrow{F}_{21}=\frac{Gm_{1}m_{2}}{r^{2}}\)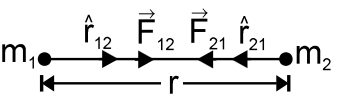
Now \(\;\;\;\hat{r}_{12}=-\hat{r}_{21},\;\;\;Thus\;\vec{F}_{21}=\frac{-Gm{1}m_{2}}{r^{2}}\hat{r}_{12}\)
Comparing above, we get \(\;\;\hat{F}_{12}=-\hat{F}_{21}\)
Gravitational Field \(\;\;\;E=\frac{F}{m}=\frac{GM}{r^{2}}\)
Gravitational Potential
Gravitational potential,
\(V=-\frac{GM}{r}\;\;\;\;\;E=-\frac{dV}{dr}\)Ring
\(V=\frac{-GM}{x\;or(a^{2}+r^{2})^{\frac{1}{2}}}\;\;\&\;\;\;E=\frac{-GMr}{(a^{2}+r^{2})^{\frac{3}{2}}}\hat{r}\;\;\;or\;\;E=-\frac{GM\;\cos\theta}{x^{2}}\)The gravitational field is maximum at a distance,
\(r=\pm a\sqrt{2}\;\;\mathbf{and\;it\;is}\;-2GM/3\sqrt{3}a^{2}\)Thin Circular Disc
\(V=\frac{-2GM}{a^{2}}\left [ \left [ a^{2}+r^{2} \right ]^{\frac{1}{2}}-r \right ]\;\;\&\;\;\;E=-\frac{2GM}{a^{2}}\left [ 1-\frac{r}{\left [ r^{2}+a^{2} \right ]^{\frac{1}{2}}} \right ]=-\frac{2GM}{a^{2}}\left [ 1-\cos \theta \right ]\)Non Conducting Solid Sphere
(a) Point P inside the sphere. \(r\leq a,\;\mathbf{then}\) \(V=-\frac{GM}{2a^{3}}(3a^{2}-r^{2})\;\&\;\;E=-\frac{GMr}{a^{3}},\)
and at the center \(V=-\frac{3GM}{2a}\;\;\&\;E=0\)
(b) Point P outside the sphere.
\(r\geq a,\mathbf{then}\;\;\;V=-\frac{GM}{r}\;\;\;\&\;\;\;E=-\frac{GM}{r^{2}}\)Uniform Thin Spherical Shell / Conducting Solid Sphere
(a) Point P inside the shell.
\(r\leq a,\mathbf{then}\;\;\;V=-\frac{GM}{r}\;\;\&\;\;\;E=0\)(b) Point P outside shell.
\(r\geq a,\mathbf{then}\;\;\;V=-\frac{GM}{r}\;\;\;\&\;\;\;E=-\frac{GM}{r^{2}}\)Variation of Acceleration Due To Gravity
Effect of Altitude
\(g_{h}=\frac{GM_{e}}{(R_{e}+h)^{2}}=g\left ( 1+\frac{h}{R_{e}} \right )^{-2}\simeq g\left ( 1-\frac{2h}{R_{e}} \right )\mathbf{when}\;h<<R\)Effects of Depth
\(g_{d}=g\left ( 1-\frac{d}{R}_{e} \right )\)Effect of the Surface of Earth
The equatorial radius is about 21 km longer than its polar radius.
We know,\(\;\;g=\frac{GM_{e}}{R_{e}^{2}}\;\mathbf{Hence}\;\;g_{pole}>g_{equator}\)
Satellite Velocity (or Orbital Velocity)
\(V_{0}=\left [ \frac{GM_{e}}{(R_{e}+h)} \right ]^{\frac{1}{2}}=\left [ \frac{gR_{e}^{2}}{(R_{e}+h)} \right ]^{\frac{1}{2}}\)When h<<Re than \(\sqrt{gR_{e}}\)
therefore, satellite velocity around earth will be \(v_{0}\sqrt{9.8\times6.4\times10^{6}}=7.92\times10^{3}\;ms^{-1}=7.92\;km\;s^{1}\)
Time Period of Satellite
\(T=\frac{2\pi(R_{e}+h)}{\left [ \frac{gR_{e}^{2}}{(R_{e}+h)} \right ]^{\frac{1}{2}}}=\frac{2\pi}{R_{e}}\left [ \frac{(R_{e}+h)^{3}}{g} \right ]^{\frac{1}{2}}\)Escape Velocity
The velocity required to escape the gravitation force or pull of a mass is given by
Ve = \(\sqrt{\frac{2GM}{R}}\)
Kepler’s Law
Following are the three of Kepler’s laws of planetary motion
First law: It states that planets go around the sun in an elliptical orbit with the sun at one of the focii.
Second Law: It states that areal velocity or area swept by a planet in a constant time is constant (dA/dt =0)
Third Law: It gives the following relation between the orbital period and semimajor axis T2 ∝ R3
So, those were some of the important gravitation formulas which would help you in your preparations for competitive examinations.
