Pythagorean Theorem

Pythagorean theorem or Pythagoras theorem is a fundamental relationship in Euclidian Geometry.  It relates three sides of a right-angled triangle.

History

The theorem is generally associated with Greek mathematician-philosopher Pythagoras and name of the theorem also comes from his name. But historical proofs tells that the theorem existed way before Pythagoras in different civilizations as well. And researchers argue that various civilizations also derived this theorem independently after Pythagoras.

Some historical works and texts having good mention about the Pythagorean triplets and the theorem itself are.

1. Babylonian tablets from circa (1900–1600 BC) is considered to be the first mention of the Pythagorean theorem.
2. Baudhayana Sulba-sutra of India (800 and 400 BC) contains a list of Pythagorean triples and a statement of the Pythagorean theorem.
3. The Nine Chapters on the Mathematical Art (A Chinese text written between 202 BC to 220 AD) have mention about Pythagorean triples.

The Theorem

Statement
The Pythagoras theorem states that the square of the side that is the hypotenuse (the side opposite to the right angle) is the sum of the square of the other two sides.

The theorem can be expressed in an equation form as follows:

c² = a² + b² (Pythagorean Equation)

where,
c is the length of the hypotenuse
a,b are the other two sides

Pythagorean Triplets

Pythagorean triplets are set of three integers wherein square of the largest integer equals the square of the other two numbers.

Examples of Pythagorean triplets.

1. 3, 4, 5
2. 5, 12, 13
3. 7, 24, 25
4. 8, 15, 17 and so on….

Proofs

As mentioned, the theorem originated with various civilizations at various times. On the same lines, the theorem also have a lot of ways to prove it. But in this tutorial let us see only two proofs of the theorems.

1. Algebraic Method

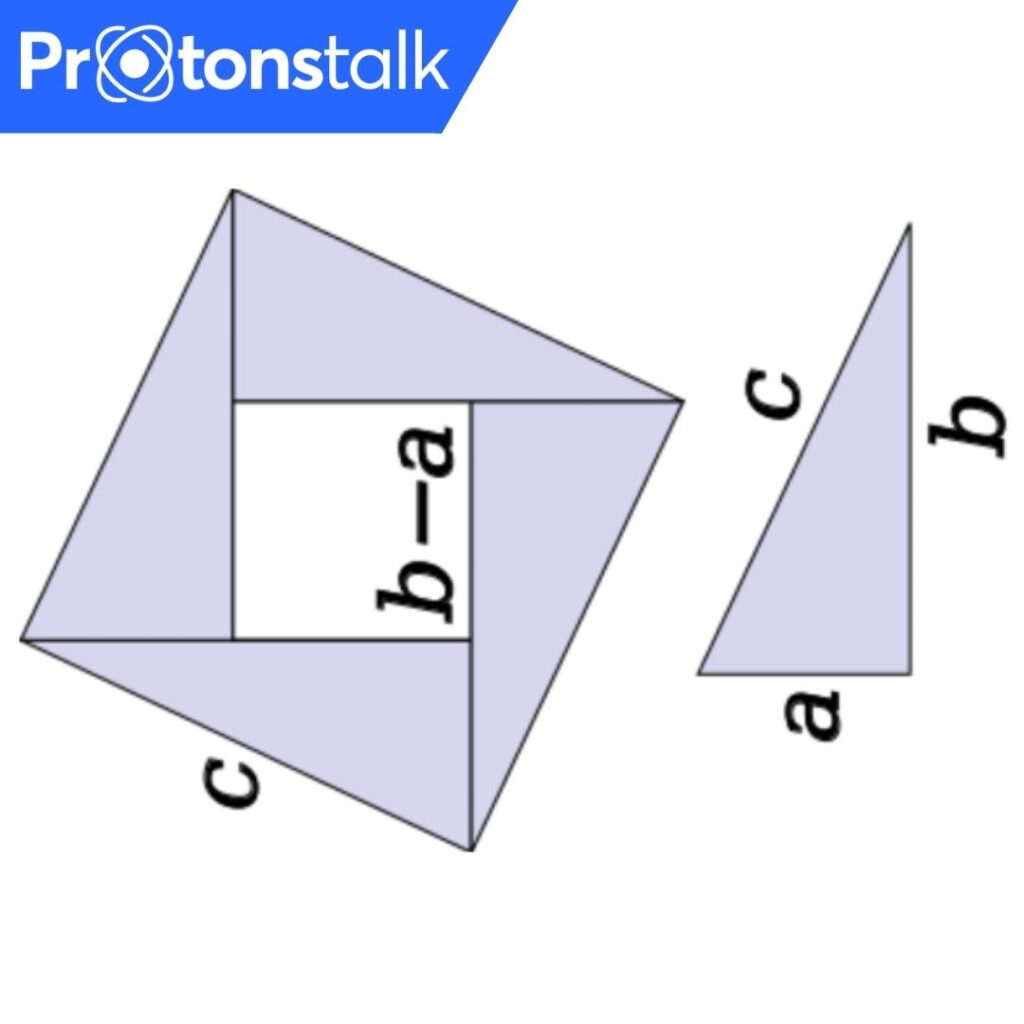
Let us consider a right-angled triangle with hypotenuse c and other two sides as a and b

Assume that we build a square using four such right angled triangles as shown in the diagram.

Now, we have to find the area of the square, first in terms of c and then in terms of a and b.

The area in terms of c
We can see that side of the square is c and we know that area of a square is square of its side. So,

=>Area = Side * Side = c*c = c²

Area in terms of a and b

Area in terms of a and b will be the square of inner square whose side is b-a and the area of four triangles.

=> Area = (b-a)² + 4(1/2*(ab)) = a² + b²

We know that, area in terms of c = area in terms of a and b.

c² = a² + b²

Hence, the Pythagorean theorem is proved.

2 Proof Using Similar Triangles

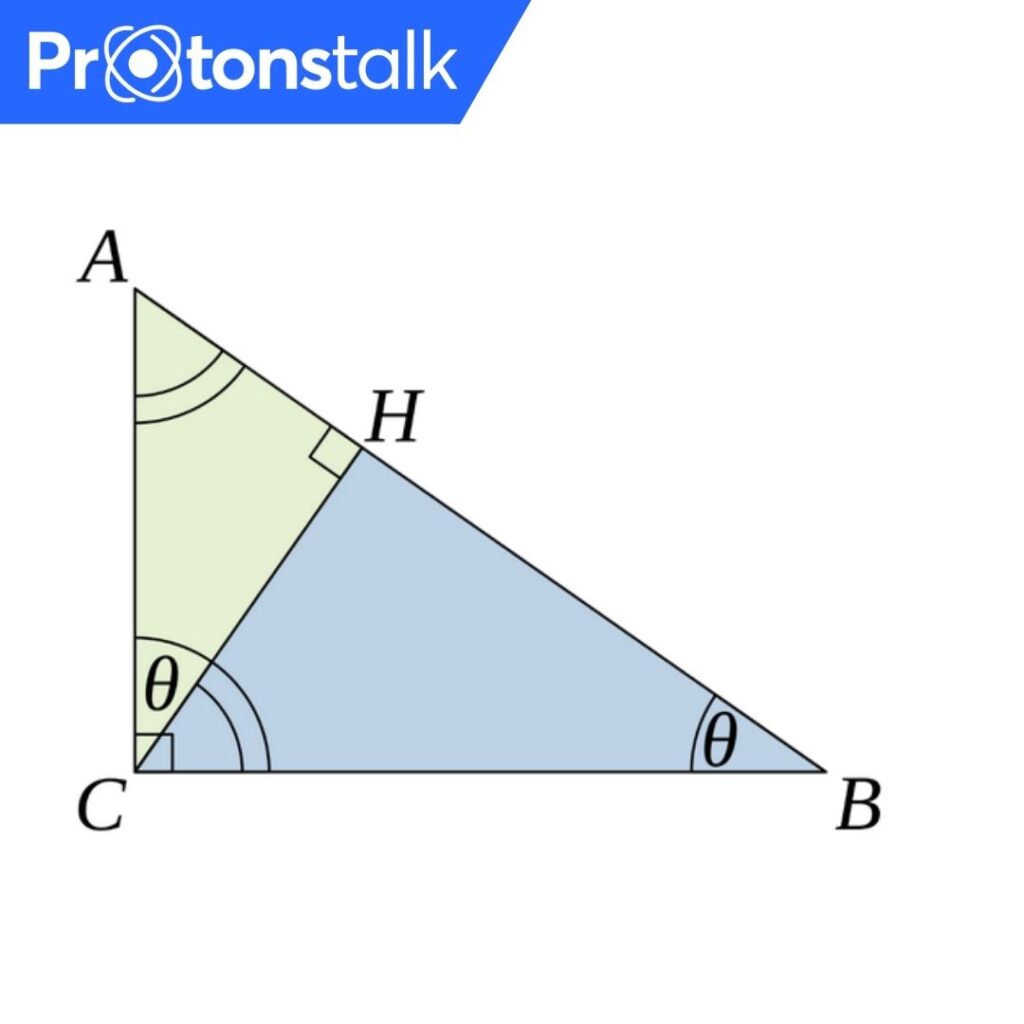
Let us consider a right-angled triangle ABC and draw and altitude from vertex C to side AB and name the intersection as H.

From similarity axioms specifically AAA similarity axiom, we can see that triangles ABC, ACH, BCH are similar.

From similarity properties we can get the following relations.

BC/AB =BH/BC (from triangles ABC, BCH)
AC/AB = AH/AC (from triangles ABC, ACH)

Cross multiplying these two equations we get,

BC² = AB * BH
AC² = AB * AH

Adding these two equations, we get

BC² + AC² = AB * BH + AB * AH
BC² + AC² = AB * (BH + AH) (BH + AH = AB)
=> BC² + AC² = AB² (Pythagorean Thoerem)

Hence Proved

Applications

1. In mathematics, the theorem is used for finding whether a triangle is right-angled, finding the hypotenuse, finding diagonal of a square and similar shapes. (Here is a Pythagorean theorem calculator if you are looking for one)

2. In daily life, we find right angles at a lot of places and at a lot of such places we use Pythagorean theorem. We use it in construction, wood work etc.

Example Problems

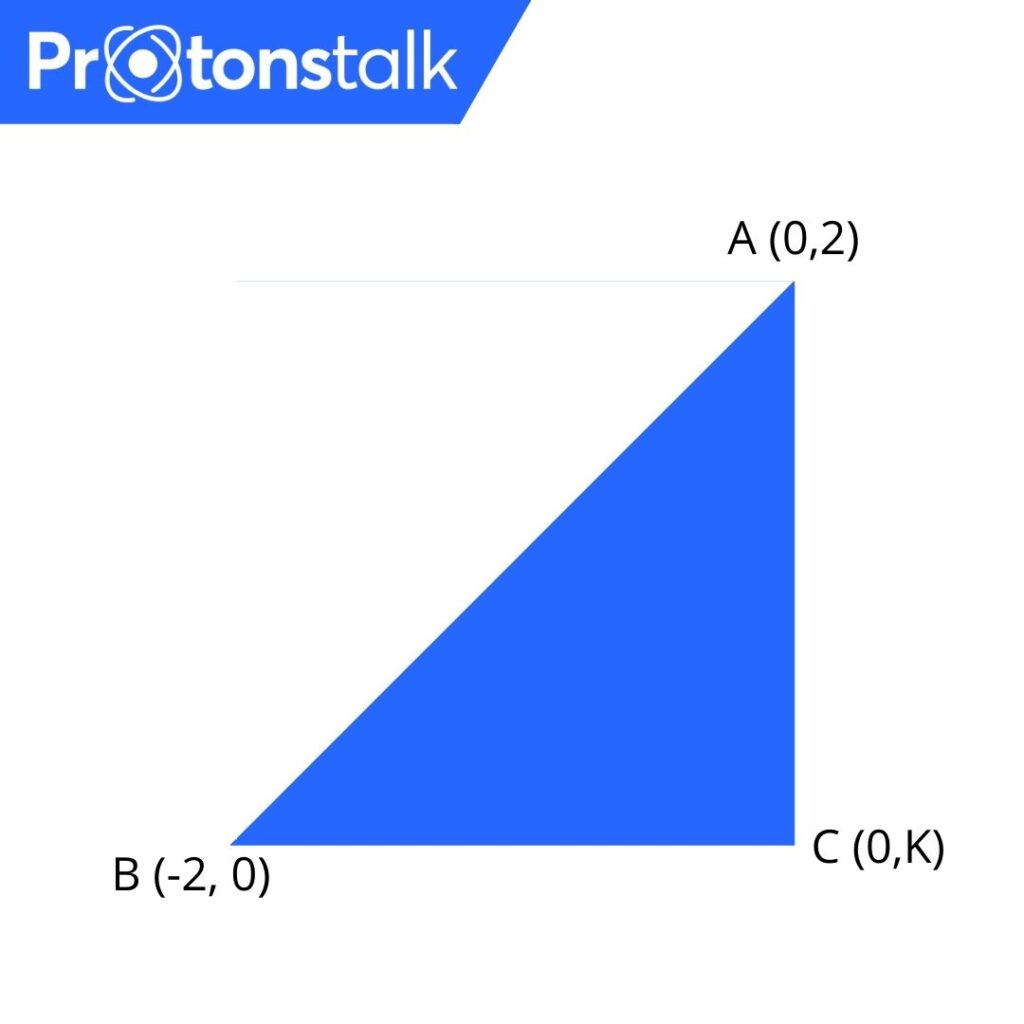
Question 1: The points A(0 , 2), B(-2 , 0) and C(0  , k) are the vertices of a right triangle with hypotenuse AB. Find k.

Ans: So, we have three vertices of a right-angled triangle but we don’t know one coordinate of third vertex C.

Here we can apply Pythagorean on the distance between three vertices and find out k

AB = √8, BC = √4+(k)² CA = √(K-2)²

Applying BC² + AC² = AB²

By substituting we find k = 0 or 2

K = 2 is not feasible solution as (0,2) is already a vertex.

So, C = (0,k) = (0,0)

Question 2: Find the perimeter of an equilateral triangle whose height is 60 cm.

Ans: As shown in the diagram, let the side of the equilateral triangle be a.

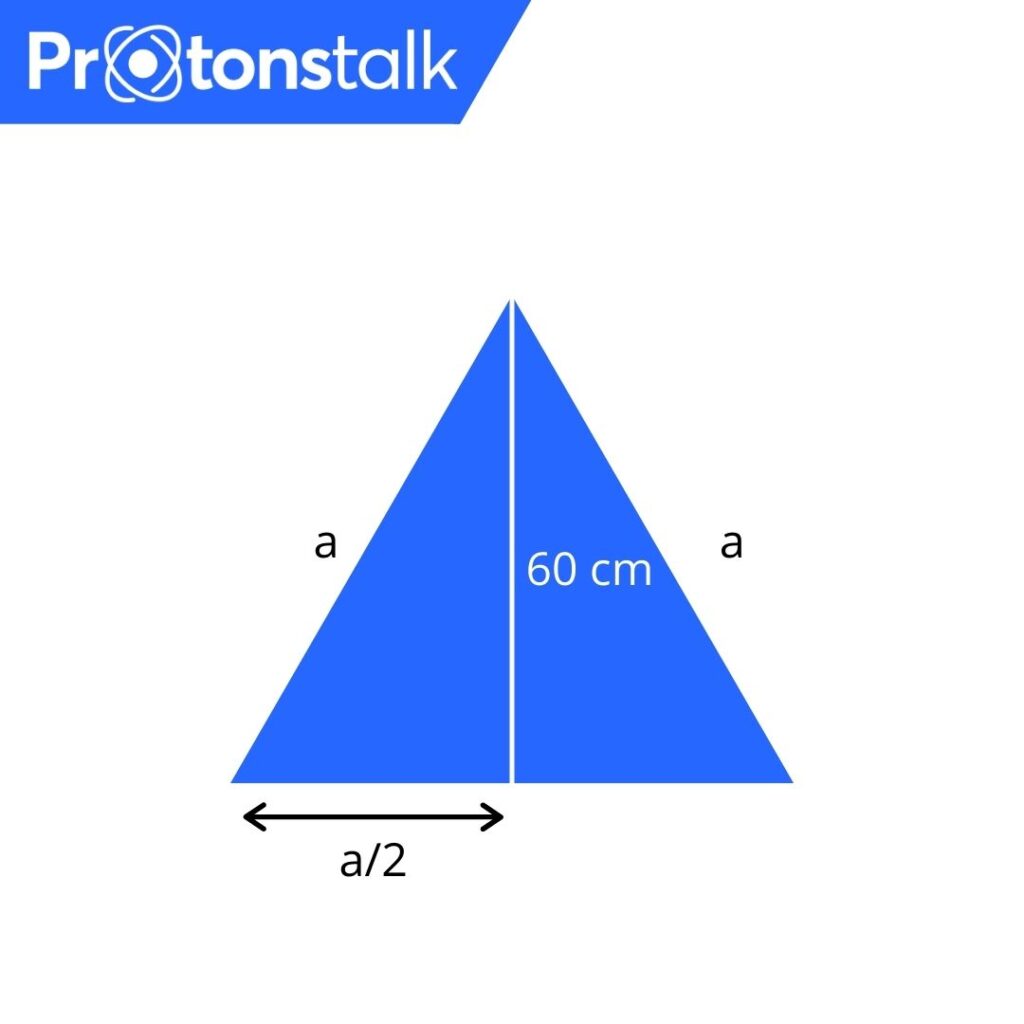
As the height of an equilateral triangle divides the base into half, the length is a/2 there and as height is also an altitude it intersects with right angle. So, half of the triangle is a right angled triangle.

So, applying Pythagorean theorem

a² = 60² + (a/2)²

Solving this, we get

a = 40√3 cm

Perimeter = 3a = 120√3 cm

FAQ