Resistance is a measure of the opposition to the flow of electrons and is calculated by dividing voltage upon current in the conductor. The dimensions of resistance can be given as \([M L^{2} T^{-3} I^{-2}]\).
Index
The Dimensions of Electrical Resistance
The dimensions of electrical resistance are: \([M][L]^{2}[T]^{-3}[I]^{-2}\)
where,
\(M \rightarrow\) Mass
\(L \rightarrow\) Length
\(T \rightarrow\) Time
\(I \rightarrow\) Electrical Current
In terms of base quantities, electrical resistance can be represented as: \(\frac{kg \ m^2}{A^2 s^3}\).
The SI unit of resistance is Ohm (\(\Omega\)).
What is Resistance?
Resistance is a measure of the opposition to the flow of electrons and the SI units of resistance is given as Ohm (\(\Omega\)).
Resistance in a cylindrical wire is given as, \(R=\frac{\rho l}{A}\)
where,
\(\rho \rightarrow\) Resistivity
\(l \rightarrow\) Length of conductor parallel to flow of current.
\(A \rightarrow\) Cross Sectional area of conductor perpendicular to the flow of electrons.
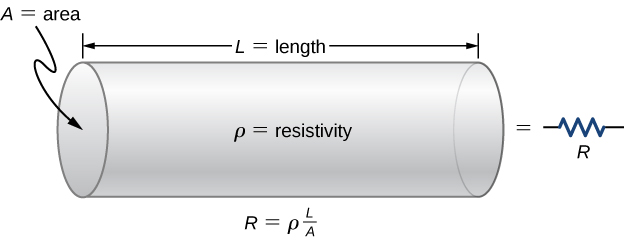
Dimensional Analysis for Resistance
It is important for any dimensional analysis problem to know some basic relations involving the quantity whose dimensions we need to find, here it is resistance.
We know from Ohm’s law: \(V = IR\)
where,
\(I\) is current and,
\(V\) is a potential difference.
Also we have, \(V = Ed\)
where,
\(E\) is electric field and,
\(d\) is distance.
Similarly, \(E = \frac{F}{q}\)
where,
\(F\) is force and,
\(q\) is charge.
Using \(I = \frac{q}{t}\)
\(E = \frac{F}{q} =\frac{F}{It}\)
So, \(R = \frac{V}{I} = \frac{Ed}{I} = \frac{Fd}{I^2 t}\)
We have,
Force \(F\) has the units \(\frac{kg m}{s^2}\) and has the dimensions \([M][L][T]^{-2}\).
\(d\) has the dimension \([L]\).
\(t\) has the dimension \([T]\).
Therefore, we have, dimensions of resistance \(R\), represented as \([R]\) is,
\([R] = \frac{[M][L][T]^{-2}[L]}{[I]^2 [T]}\)
\([R] = [M][L]^{2}[T]^{-3}[I]^{-2}\)
Example Problems
Question 1. Derive the dimensional formula for resistivity \(\rho\).
Solution. We have,
\(R=\frac{\rho l}{A}\)
\(\rho=\frac{R A}{l}\)
\([\rho ]=\frac{[R] [A]}{[l]}\)
Also, we have,
\([A] =[m^2] = [L]^2\)
\([l] = [m] = [L]\)
\([R] = [M][L]^{2}[T]^{-3}[I]^{-2}\)
Therefore,
\([\rho ]=\frac{ [M][L]^{2}[T]^{-3}[I]^{-2} [L]^2}{[L]}\)
\([\rho ]= [M][L]^{3}[T]^{-3}[I]^{-2}\)
Hence, the dimensional formula for resistivity is \([M][L]^{3}[T]^{-3}[I]^{-2}\).
Question 2. Derive the dimensional formula for Voltage \(V\).
Solution. We have from Ohm’s law,
\(V=IR\)
\([V]=[I][R]\)
Also, we have, \([R] = [M][L]^{2}[T]^{-3}[I]^{-2}\)
Therefore,
\([V]=[I][M][L]^{2}[T]^{-3}[I]^{-2}\)
\([V]=[M][L]^{2}[T]^{-3}[I]^{-1}\)
FAQs
The dimensional formula for electrical resistance is: \([M][L]^{2}[T]^{-3}[I]^{-2}\)
where,
\(M \rightarrow\) Mass
\(L \rightarrow\) Length
\(T \rightarrow\) Time
\(I \rightarrow\) Electrical Current
In terms of base quantities, electrical resistance can be represented as: \(\frac{kg \ m^2}{A^2 s^3}\).
The SI unit of resistance is Ohm(\(\Omega\)).
Resistance of a wire can be expressed as, \(R=\frac{\rho l}{A}\)
where,
\(\rho \rightarrow\) Resistivity
\(l \rightarrow\) Length of conductor parallel to flow of current.
\(A \rightarrow\) Cross-Sectional area of conductor perpendicular to the flow of current.
Hence, resistance increases with an increase in resistivity (depends upon the material), with an increase in length of conductor l. Resistance decreases with an increase in the cross-sectional area of the conductor.
Resistivity depends upon
– Temperature: Resistivity usually increases with the increase in temperature for metals.
– Composition: Different Alloys have different resistivity.
– Mechanical stress and strain also affect resistivity to some extent.
Conductance \(G\) is the reciprocal of resistance \(R\).
\(G = \frac{1}{R}\)
Dimensions of conductance are \([M]-1 [L]^{-2}[T]^{3}[I]^{2}\).
While, conductivity \(\sigma\) is the reciprocal of resistivity.
\(\sigma = \frac{1}{\rho}\)
The dimensions of conductivity are \([M]-1 [L]^{-3}[T]^{3}[I]^{2}\).
Related Topics:
