Rolle’s Theorem

Rolle’s Theorem is a special case of the mean-value theorem of differential calculus.

It expresses that if a continuous curve passes through the same y-value, through the x-axis, twice, and has a unique tangent line at every point of the interval, somewhere between the endpoints, it has a tangent parallel x-axis.

Rolle’s theorem states that,
Let function \(f(x)\) is a real valued, continuous on the closed interval \([p, q]\) and differentiable on the open interval \((p, q)\), then 

if \(f(p) = f(q)\), 

then there exists at least one point ‘s’ in the open interval \((p, q)\) for which \(f’(s)= 0\).

History

Bhāskara II (1114–1185), an Indian mathematician,  is believed with knowledge of Rolle’s theorem.

In 1691 Michel Rolle gave proof, but it only covered the case of polynomial functions, and the theorem was named after Michel Rolle.

In 1823, Cauchy first proved the theorem as a corollary of proof of the mean value theorem. 

In 1834, Moritz Wilhelm Drobisch of Germany first used the name “Rolle’s theorem” and again by Giusto Bellavitis of Italy in 1846.

Rolle’s Theorem Explained

If a function \(f(x)\) is continuous on the closed interval \([p, q]\) and differentiable on the open interval \((p, q)\), then 

if \(f(p) = f(q)\), 

then there exists at least one point ‘s’ in the open interval \((p, q)\) for which \(f’(s)= 0\).

Rolle’s theorem is used to prove the MVT, of which Rolle’s theorem is a special case.

The stated hypothesis of the Mean Value Theorem guarantees the existence of a point ‘s’ with

\(f’(s) = \frac{f(q) – f(p)}{q – p} = 0\)

Let’s consider a real-valued, continuous function \(f\) on a closed interval \([p,q]\) with \(f (p) = f (q)\). 

If for every \(x\) in the open interval \((p, q)\) the right-hand limit

\(f'(x^{+}):=\lim _{h\to 0^{+}}\frac {f(x+h)-f(x)}{h}\)

and the left-hand limit

\(f'(x^{-}):=\lim _{h\to 0^{-}}\frac {f(x+h)-f(x)}{h}\)

exist in the extended real line \([−\infty, \infty]\), then there is some number ‘s’ in the open interval \((p, q)\) such that one of the two limits

\(f'(s^{+}) \quad {\text{and}} \quad f'(s^{-})\) 

is \(\geq 0\) and the other one is \(\leq 0\) (in the extended real line). 

If the left and right-hand limits agree for every \(x\), they also agree in particular for ‘s.’ Hence the derivative of \(f\) will exist at ‘s’ and is equal to zero.

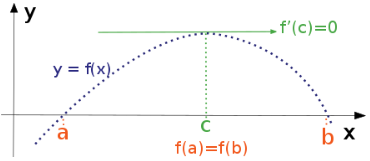
Geometrical Representation of Rolle’s Theorem 

In the given graph, the curve \(y = f(x)\)  is continuous between \(x = a\)  and \(x = b\). At every point, it is possible to draw a tangent and ordinates corresponding to the abscissa within the interval and are equal. 

Then, there is at least one tangent to the curve that is parallel to the x-axis.

Algebraically, this theorem tells us that if \(f(x)\) is represented by a polynomial function in \(x\) and the two roots of the equation \(f(x) = 0\) are \(x = a\) and \(x = b\). Then, at least one root of the equation \(f‘(x) = 0\) lying between these values.

The converse of Rolle’s theorem is not valid, and it is also possible that there exists more than one value of x, for which the theorem holds good, but there is a definite chance of the existence of one such value.

Applications

• MVT, along with Rolle’s Theorem, is used limit calculation and routinely employed in calculus problems.

Questions

Question 1. Let \(f(x) = x^2 + 2x\). Find all values of \(c\) in the interval [-2, 0] such that \(f’(c) = 0\).  

Solution. Firstly, does the function \(f(x)\) satisfies all the conditions of Rolle’s theorem.

• f(x) is continuous in [-2,0] as the function;
• It is differentiable everywhere over the open interval (−2,0);
• \(f(−2) = (−2)^2 + 2 * (−2) = 0\), and \(f(0) = 0 * 2 + 2 * 0 = 0\),

⇒ f(−2) = f(0).

Hence it is true for Rolle’s theorem.

Therefore, \(f′(x) = (x^2 + 2x )′ = 2x + 2\)

And, \(f′(c) = 2c + 2 = 0\),

⇒ c = −1.

Thus, \(f′(c) = 0\) for \(c = −1\).

Question 2. Check the validity of Rolle’s theorem for the function \(f(x) = x^2 − 6x + 8\).

Solution. Roots of given quadratic function x = 2 & 4.

Then by Rolle’s theorem, 

there must be a point ‘c’ in the interval (2,4) where the derivative of the function f(x) equals zero.

\(f′(x) = (x^2 − 6x + 8)′ = 2x − 6\).

It is equal to zero at the following point x = c:

\(f′(x) = 0\),
⇒ \(2x − 6 = 0\),
⇒ \(x = c = 3\).

Therefore c = 3 belongs to the interval (2,4).

FAQs