Mean Value Theorem

Mean value theorem (MVT) states that,

Let \(f\) be a real function defined on the closed interval [a , b]; a < b, such that:

1. f is continuous over the closed interval [a, b] and
2. f is differentiable over the open interval (a, b)

then, there exists a \(c \in  [a, b]\), such that

\(f'(c) = \frac{ f(b) – f(a)}{b – a}\)

where \(f'(c)\) is the value of derivative at \(x = c\).

Augustin Louis Cauchy gave the modern form of the mean value theorem in 1823.

History 

A special case of Mean Value Theorem was first observed in the commentaries given by Parameshwara on Govindasvami and Bhaskara II (around 1400 A.D.).

Around 1690 A.D., Michel Rolle proved Rolle’s theorem (based on MVT) for polynomials. After this, Euler and Lagrange made efforts to establish Rolle for other functions and hence MVT.

In 1823 A.D. Cauchy proved MVT for \(C^1\) functions.

Formal Statement Of Mean Value Theorem

Let \(f:[ a, b ]  \rightarrow \mathbb{R}; a<b\) be a continuous real function on \([a, b]\) and differentiable on \((a, b)\) then, 

\(\exists c \in [a, b]\) such that

\(f'(c) = \frac{ f(b) – f(a) }  { b – a }\)

where, \(f'(c) = \frac{df}{dx} | _{x=c}\)

Mean Value Theorem transforms to Rolle’s Theorem for the case when \(f(a) = f(b)\).  \(f'(c) = 0\) for this case. In this sense, it could be said that the mean value theorem is more general, and Rolle arises as a special case.

Geometrical Meaning of MVT

Mean Value Theorem looks more obvious when analyzed geometrically. 

Consider a 2D cartesian coordinate system. Let \(y = f(x)\) denote our continuous and differentiable real function. Let \(A\) be the point corresponding to the lower limit of our interval and \(B\) be the point corresponding to the upper limit of our interval, i.e., 

\(A = (a, f(a))\) and \(B = (b, f(b))\)

Draw a straight line connecting \(A\) and \(B).

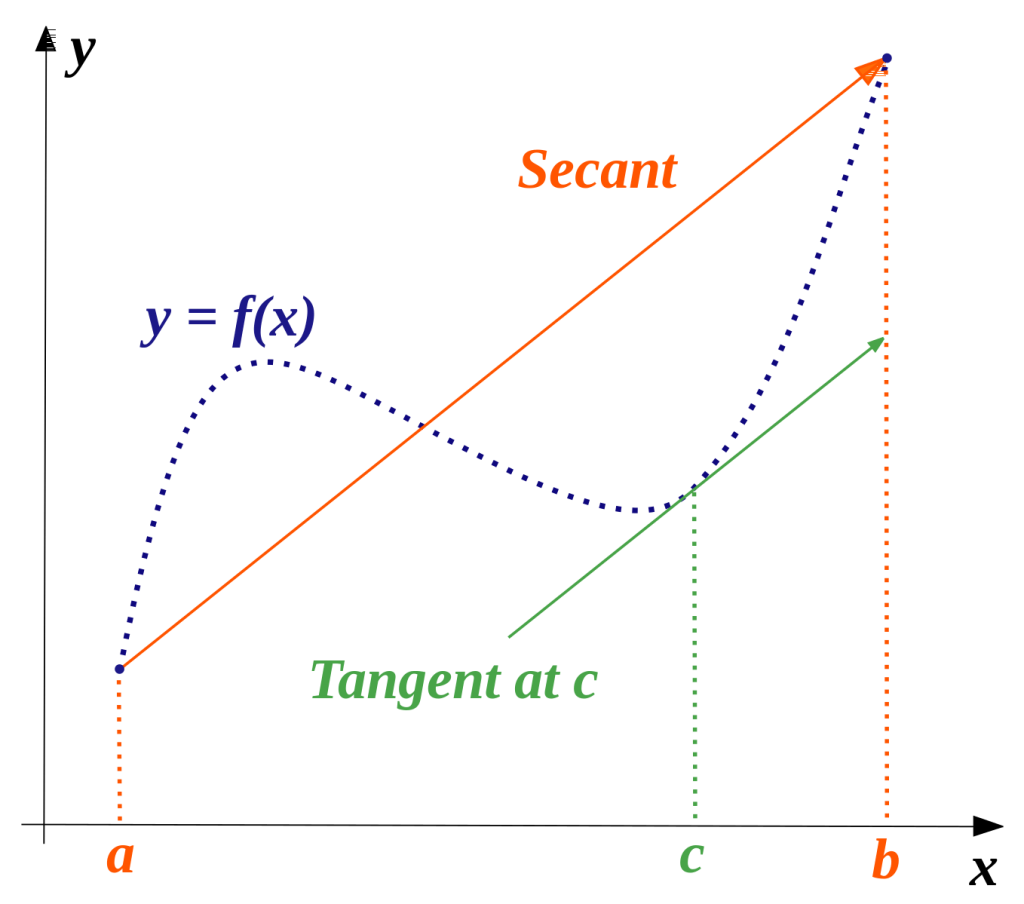
This line is called secant to the curve \(y = f(x)\) between \(A\) and \(B\). The slope of the secant:

Slope of secant = \(\frac{y_2 – y_1 }{x_2 – x_1} = \frac {f(b) – f(a) }{b – a}\)

We know that the slope of the tangent of a curve at a point is the value of the derivative at that point.

By Mean Value Theorem, there exists at least one point where the tangent to the curve becomes parallel to the secant. In other words, the slope of the tangent becomes equal to the slope of the secant at some point.

Proof of Mean Value Theorem

Mean Value Theorem can be proved by using Rolle’s Theorem as a lemma.

Rolle’s Theorem : \(Let f:[ a, b ]  \rightarrow \mathbb{R}; a<b\) be a continuous real function on \([a, b]\) and differentiable on \((a, b)\)  and \(f(a) = f(b)\), then 

\(\exists c \in [a, b]\) such that \(f'(c) = 0\).

Let, \(g(x) = f(x) – k x\) ,
where \(k \in \mathbb{R}\) is a constant.

Fix the value of \(k\) such that \(g(x)\) follows Rolle’s theorem:

\(g(a)= g(b)\)
\(\Rightarrow   f(a) – k a = f(b) – k b\)
\(\Rightarrow   k a – k b = f(b) – f(a)\)
\(\Rightarrow   k = \frac{f(b)-f(a)}{b-a}\)

By Rolle’s Theorem, \(\exists c \in [a, b]\) such that \(g'(c) = 0\)

We have,

\(g'(x) = f'(x) -k\)
\(\Rightarrow f'(x) = g'(x) + k\)
\(\Rightarrow f'(c) = g'(c) + k\)
\(\Rightarrow f'(c) = k\)
\(\Rightarrow f'(c) = \frac{f(b)-f(a)}{b-a}\)

Cauchy’s Form of Mean Value Theorem

A useful, modified form of Mean Value Theorem is the Cauchy’s Mean Value Theorem.

Let \(f(x)\) and \(g(x)\) be two real functions such that:

1. \(f(x)\) and \(g(x)\) both are continuous over the same closed interval \([a, b]\) 
2. \(f(x)\) and \(g(x)\) both are differentiable over the same open interval \((a, b)\) 

then, \(\exists c \in (a, b)\) such that, 

\(( f(b) – f(a) ) g'(c) = ( g(b) – g(a) ) f'(c)\) 

When \(g(b) \neq g(a)\) and \(g'(c) \neq 0\)  , this is equivalent to 

\(\frac{f'(c)}{g'(c)} = \frac{ f(b) – f(a)}{g(b)-g(a)}\)

Proof of Cauchy’s Mean Value Theorem

Cauchy’s Mean Value Theorem can also be proved by Rolle’s theorem.

Assuming \(g(b) \neq g(a)\), define 

\(h(x) = f(x) – k g(x)\)

where \(k \in \mathbb{R}\) is a constant.

Fix \(h(x)\) so that it follows Rolle’s theorem, i.e., 

\(h(b) = h(a)\)
\(\Rightarrow f(b) – k g(b) = f(a) – k g(a)\)
\(\Rightarrow k g(b) – k g(a) = f(b) – f(a)\)
\(\Rightarrow k =\frac{ f(b) – f(a) }{ g(b) – g(a) }\)

From Rolle’s theorem, we have

\(h'(c) = 0 ; c \in [a, b]\) 

we know, 

\(h'(x) = f'(x) – k g'(x)\)
\(\Rightarrow h'(c) = f'(c) – k g'(c)\)
\(\Rightarrow 0 = f'(c) – k  g'(c)\)
\(\Rightarrow \frac{f'(c)}{g'(c)} = k\)
\(\Rightarrow \frac{f'(c)}{g'(c)} = \frac{ f( b )- f(a) }{ g(b) – g(a) }\)

Examples

Question 1. Let the function, \(f:[-7, 0] \rightarrow \mathbb{R}\)  be continuous on \([−7, 0]\) and differentiable on \((−7, 0)\). If \(f(−7) = −3\) and \(f'(x) ≤ 2\), for all \(x \in  (−7, 0)\), then for all such functions \(f\) , \(f (−1) + f (0)\) lies in the interval:

1. [-6, 20]
2. (\(-\infty\), 20]
3. (\(-\infty\), 11]
4. [-3, 11]

Solution. Applying MVT in the interval [-7, 0],

\(f'(c) = \frac{f(0)-f(-7)}{0-(-7)}\)

\(f'(c) = \frac{f(0) +3}{7}\)

Also, \(f'(c) \leq 2\)

\(\Rightarrow \frac{f(0) +3} {7} \leq 2\)
\(\Rightarrow f(0) + 3 \leq 14\)
\(\Rightarrow f(0) \leq 11\)

Again, applying MVT in the interval [-7, -1],

\(f'(c) = \frac{f(-1) – f(-7)}{-1+7}\)

\(f'(c) = \frac{f(-1) + 3} { 6}\)

Also, \(f'(c) \leq 2\)

\(\Rightarrow \frac{f(-1) +3}{6} \leq 2\)
\(\Rightarrow f(-1) \leq 12-3\)
\(\Rightarrow f(-1) \leq 9\)

Therefore, \(f(-1)+f(0) \leq 20\). So the answer is 2) (\(-\infty\), 20]

Question 2. If \(f(1)  =  10\) and \(f'(x)  \geq 2\) for \(1 \leq x \leq 4\) how small can \(f (4)\) possibly be ?

Solution. Applying MVT in the interval [1,4],

\(f'(c) = \frac{f(4) – f(1)}{4-1}\)

\(\Rightarrow f'(c) = \frac{f(4) – 10} {3}\)

Also, \(f'(c) \geq 2\)

\(\Rightarrow \frac{f(4) – 10} {3} \geq 2\)
\(\Rightarrow f(4)  \geq 6+10\)
\(\Rightarrow f(4) \geq 16\)

Therefore the minimum \(f(4)\) can get is \(f(4) = 16\).

Applications

1. MVT can be used to prove L’Hopital’s rule and similar theorems.

2. MVT is used routinely in real analysis and geometry. It should be noted that MVT is invalid for Complex functions.

3. MVT, along with Rolle’s Theorem, is used limit calculation and routinely employed in calculus problems.

FAQs