The mass of an electron is \(9.1093837015 \ \times \ 10^{-31} \ kg\). This is called the rest mass of the electron. The rest mass of electrons is denoted as \(m_e\). According to Einstein’s special theory of relativity, the mass of an electron increases when it is in motion.
Mass of an electron: \(9.1093837015 \ \times \ 10^{-31} \ kg\)
If this mass were fully converted into energy, the energy would be 0.511 MeV(Mega electronVolts).
Index
History
Today there are multiple ways to determine the rest mass of an electron. Historically, the mass of the electron was deduced from the result of two different experiments: The cathode ray tube experiment by J. J. Thomson and Millikan’s oil drop experiment.
The cathode ray tube experiments determined the charge-to-mass ratio of electrons. Millikan’s oil drop experiment found the charge of the electron. Combining the results from the two experiments, the mass of the electron was calculated.
Cathode Ray Experiment
Before J. J. Thomson, Cathode ray experiments were carried out by Sir Arthur Schuster. It was J. J. Thomson who identified that the cathode rays are beams of particles called electrons.

For this discovery, he was awarded the Nobel prize in 1906. He calculated the charge-to-mass ratio of electrons to good precision in the cathode ray experiment.
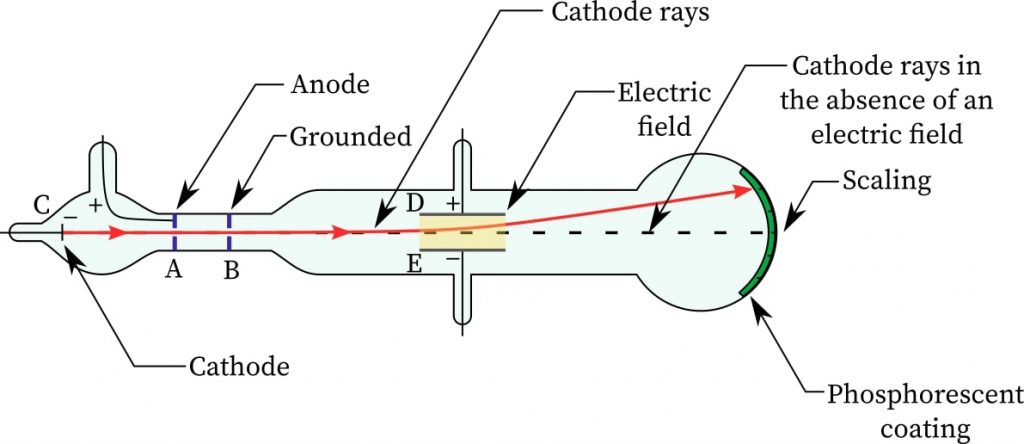
The experimental setup uses a device called the cathode ray tube (refer the fig 1). The cathode is heated, and it ejects electrons via thermionic emission. The electrons move towards the anode with a reasonable velocity.
A hole in the anode plate allows a beam of electrons to pass through. This beam of electrons is called Cathode Ray. This beam is deflected by the deflecting metal plates D and E in the figure.
The deflected beam strikes the circular screen, which is covered with a phosphorescent material. When the beam falls on the phosphorescent material, its energy gets converted into light energy. A bright spot is seen on the screen at the same point. The screen is scaled, so that amount of deflection can be measured.
The force on the electron due to the electric field is
\( F = eE = m_e a \) \( a= \frac{e}{m_e} E \)which is the acceleration. Noting the amount of deflection and the electric field, the ratio \( \frac{e}{m_e} \) is found to be \( 1.75882 \ \times \ 10^{11} \) C/kg.
Millikan’s Oil Drop Experiment
Millikan’s oil drop experiment determined the charge of an electron. The experiment was performed by Robert A. Millikan and Harvey Fletcher in 1909. Millikan was awarded the Nobel prize in 1923.
The experimental setup consists of an
1. Atomiser (an oil spray which produces very fine oil droplets)
2. Two metal plates
3. A travelling microscope
4. A high voltage power supply
5. An X-ray source
6. A container/cover.
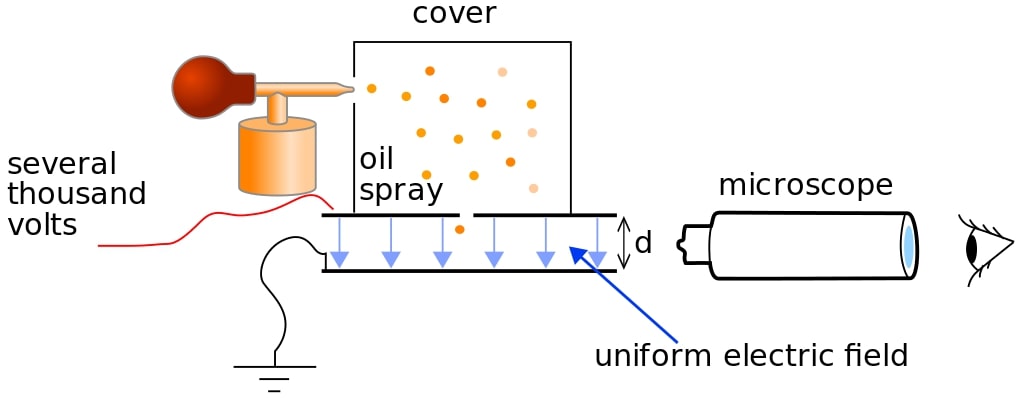
The atomiser sprays very fine oil droplets into the container, where they ionized by X-Ray. The droplets acquire charges as a result of this ionisation. Different droplets acquire different charges. The droplets start falling under the effect of gravity and attain terminal velocity. At terminal velocity, the force of viscosity and the buoyant force is equal to the gravitational force.
\( F_g = F_{visc} +F_{buoyant} \)=> \( m_{drop} g = 6 \pi r \eta v + m_{air} g \)
where
\(m_{drop} \) is the mass of an oil drop
\( m_{air}\) is the mass of air displaced by the oil drop
\( r\) is the radius of a drop
\( \eta\) is the viscosity of air
\( v\) is the terminal velocity.
=> \(m_{air} = \frac{4}{3} \pi \rho r^3 \)
We assume that the drops are spherical. So, we have,
\( \frac{4}{3} \pi ( \rho_{oil} – \rho ) r^3 g = 6 \pi r \eta v\)The terminal velocity of the drop is found by observation through the travelling microscope. Hence, in this way, the radius of the drop is found.
Now, the electric field on the metal plates is turned on. The field is adjusted such that the charged drop stays suspended at a place in the air. When this happens, the viscous force becomes zero due to the zero velocity. So to balance the force, an equal force is applied through the electric force.
\( qE = 6 \pi r \eta v\)The value of q is found to be a small integer multiple of ‘e’, the value of the charge of an electron.
\( e = – 1.60217 \ \times \ 10^{-19} \ C\)How the mass was calculated?
We know the \( \frac{e}{m_e} \) ratio from the cathode ray experiment and \( e \) from the Millikan’s oil drop experiment.
The mass of the electron then is
\( m_e = \frac{e}{\frac{e}{m_e}} = \frac{1.60217 \ \times \ 10^{-19}}{1.75882 \ \times \ 10^{11}} kg \) \(m_e = 9.1093837015 \ \times \ 10^{-31} \ kg\)FAQs
The relative mass of an electron is the mass of an electron w.r.t the mass of a proton. The relative mass of a proton is 1. The relative mass of an electron is \(\frac{1}{1836}\).
The charge of the electron was determined by Robert A. Millikan. Historically, the mass of the electron was deduced from the result of two different experiments:
1. The cathode ray tube experiment by J. J. Thomson and
2. Millikan’s oil drop experiment.
The cathode ray tube experiments determined the charge to mass ratio of electrons.
Millikan’s oil drop experiment found the charge of the electron. Combining the results from the two experiments, the mass of the electron was calculated.
The mass of an electron is \( 9.1093837015 \ \times \ 10^{-31} \ kg \). This is called the rest mass of the electron. The rest mass of electrons is denoted as \(m_e\).
According to Einstein’s special theory of relativity, the mass of an electron increases when it is in motion.
If this mass were fully converted into energy, the energy would be 0.511 MeV(Mega electronVolts).
References:
